SketchUp
The Golden Ratio
The Golden Ratio, Golden Mean, or Golden Section, is a number often encountered when taking the ratios of distances in simple geometric figures such as the pentagon, pentagram, decagon and dodecahedron. It is sometimes referred to as φ, or Phi. The decimal representation of phi is 1.6180339887499... .
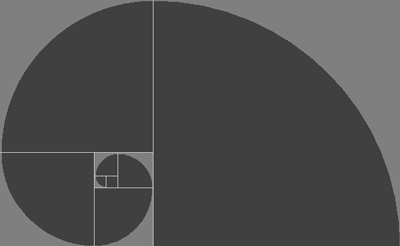
Given a rectangle having sides in the ratio 1:x, φ is defined as the unique number x such that partitioning the original rectangle into a square and new rectangle results in a new rectangle which also has sides in the ratio 1:x. Such a rectangle is called a golden rectangle, and successive points dividing a golden rectangle into squares lie on a logarithmic spiral, giving a figure known as a whirling square.
In other words, if you have a rectangle whose sides are related by phi you can create a new rectangle by 'swinging' the long side around one of its ends to create a new long side. The new rectangle is also Golden. If you start with a square (1 x 1) and start swinging sides to make rectangles, the result will be Golden rectangles:
1 x 1
2 x 1
3 x 2
5 x 3
8 x 5
13 x 8
21 x 13
34 x 21
and so on, with, again, each addition coming ever closer to multiplying by phi.
Making Golden Rectangle
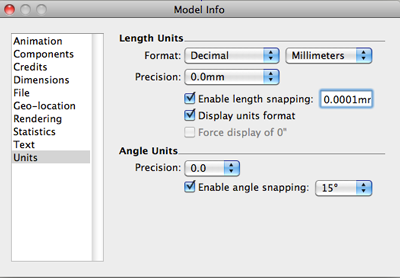
- Select Window>Model Info

- Change the format to Decimal and Millimeters:
- Change to Top View
-
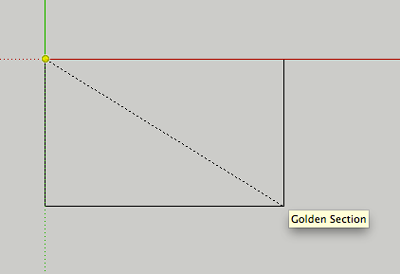
Select the Rectangle Tool. Drag the rectangle tool from the origin out until you see the diagonal line and the words Golden Section pop up
- To find out the dimensions, CTRL+click on a segment and choose entity info
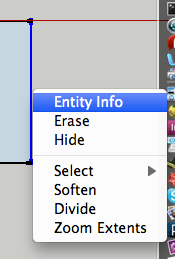
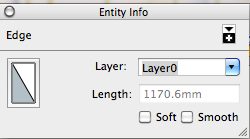
- Do the same for the other segment:
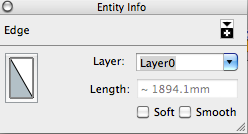
- Use a calculator to determine the ratio.
1170.6/1894.1=.61802439153
- Drag the rectangle tool to draw a square within the rectangle:
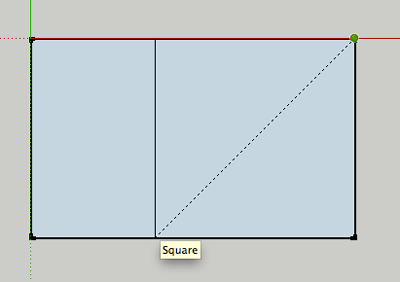
-
If you keep dividing, you'll end up with a spiral
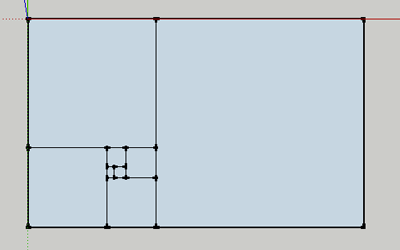
The Fibonacci Series and the Golden Rectangle
Fibonacci (short for Filius Bonacci -son of Bonacci-, Leonardo da Pisa) (1175-1250)
was a European mathematician during the middle ages.
Italian and born in Pisa, Italy, Fibonacci grew up with a North African
education under the Moors, travelled extensively and learned the Hindu-Arabic system of
arithmetics. He was one of the
first people to introduce the Hindu-Arabic number system (the positional system we use today)
to Europe. One of the problems in his book
Liber Abbaci,
was the problem about rabbits
in a field which introduced the Fibonacci series:
1, 1, 2, 3, 5, 8, 13, 21, etc. In this
series the n-th Fibonacci number is the sum of the (n-1)th and the (n-2)th numbers.
It was the French mathematician
Edouard Lucas (1842-1891) who gave the name
Fibonacci
numbers to this series and found many other important applications of them.
The original problem that Fibonacci investigated (in the year 1202) was about how fast
rabbits could breed in ideal circumstances.
Suppose a newly-born pair of rabbits, one male, one female, are put in a field.
Rabbits are able to mate at the age of one month so that at the end of its second month a
female can produce another pair of rabbits. Suppose that the rabbits never die and that
the female always produces one new pair (one male, one female) every month from the
second month on. The puzzle that Fibonacci posed was...
How many pairs will there be in one year?
- At the end of the first month, they mate, but there is still one only 1 pair.
- At the end of the second month the female produces a new pair, so now there are 2 pairs of rabbits in the field.
- At the end of the third month, the original female produces a second pair, making 3 pairs in all in the field.
- At the end of the fourth month, the original female has produced yet another new pair, the female born two months ago produces her first pair also, making 5 pairs.
The number of pairs of rabbits in the field at the start of each month is 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
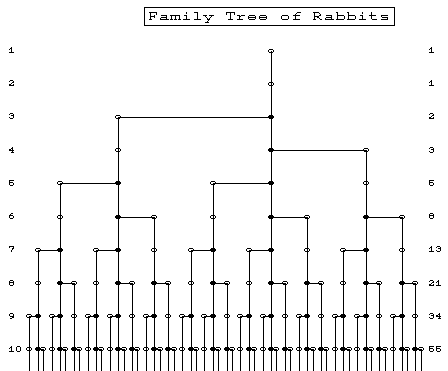
The
golden ratio is obtained by taking the ratio of successive terms in the Fibonacci series:
- 2/1 = 2
- 3/2 = 1.5
- 5/3 = 1.6666...
- 8/5 = 1.6
- 13/8 = 1.625
- 21/13 = 1.61538...
- 34/21 = 1.61904...
and so on, with each addition coming ever closer to multiplying by some as-yet-undetermined number.
The number that this ratio is oscillating around is
phi (1.6180339887499...).
 |
if you start with two small squares of size 1 next to each other.
On top of both of these draw a square of size 2 (=1+1).
You can now draw a new square - touching both a unit square and the latest square of side 2 - so having sides 3 units long; and then another touching both the 2-square and the 3-square (which has sides of 5 units). You can continue adding squares around the picture, each new square having a side which is as long as the sum of the latest two square's sides . This set of rectangles whose sides are two successive Fibonacci numbers in length and which are composed of squares with sides which are Fibonacci numbers, or Fibonacci Rectangles.
|
Here is a function using the formula attributed to both Binet and de Moivre:
function fibonacci(theNumber) {
var Phi= (1+ Math.sqrt(5))/2; // The Golden section constant
return (Math.round((Math.pow(Phi, i)/Math.sqrt(5))));
}












