Fractals
Introduction
A fractal is fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole. The term fractal was coined by Benoît Mandelbrot in 1975 and was derived from the Latin fractus meaning broken or fractured. A mathematical fractal is based on a recursive equation. There are several examples of fractals, which are defined as portraying exact self-similarity, quasi self-similarity, or statistical self-similarity. While fractals are a mathematical construct, they are also found in nature.
2D line-division type fractals are easy to create on the MakerBot. Recursive algorithms can neatly define the act of repeatedly inserting a sequence in between copies of itself to generate the Coch Curve and other related shapes.
3D fractals, like the Serpinski sponge, aren't as easy to create. The Serpinski sponge in particular has overhangs that will make it poorly suited for printing on a non-support printer, and although the self-similar nature of fractals may make it plausible to make 3D fractals which by construction do not need supports, the added complexity of the formulas, coupled with their lack of innate suitability to the plotting method will cause some trouble.
Mathematica
Artist and mathematician, George Hart taught a course at Stony Brook University in Fall 2007 that covered procedural generation of three-dimensional forms, with an emphasis on making triangulated manifold boundaries suitable for solid freeform fabrication (SFF).
Hart uses Mathematica to generate his models.
Introduction to Mathematica
To start a new program in Mathematica, create a new Notebook. A notebook is the main window for entering input and for displaying resultsTo enter input, just start typing. You can create, save, open and close a notebook using the File menu.
Notebooks are organized into units called cells. These cells are identified by the brackets on the right hand side.The insertion point is indicated by a horizontal line that appears after your output; it is called the cell insertion bar . This is where a new cell will appear after you start typing.Move the cursor in your notebook window until it becomes a horizontal I-beam.
To create a text cell, get a cell insertion bar. Then choose Format >Style >Text or use the keyboard shortcut Alt+7 (Command+7 on Mac).
To evaluate input, press SHIFT+ENTER.
Mathematica supports standard mathematical operations. In addition to using * for multiplying, you can just separate numbers by a space. So xy is not the same as x y
Calculations in Mathematica are done by calling functions. The most general way to enter a function is to give the name of the function followed by square brackets that enclose the argument or arguments of the function. If a function has more than one argument, the arguments are separated by commas.The function N is used to give numerical approximations to its first argument:
N[Pi,50]
{x, 0,20}
{2, 4, 6} + {100, 40, 15}Mathematica is case sensitive and the names of built-in functions are always capitalized.
Function arguments are enclosed in square brackets and are separated by commas.
Like other programming languages, you can assign values to variables like this:
x=10;
?x
Clear[x]
The Mathematica Documentation Center is the main interface to documentation in Mathematica. Open the documentation by going to the Help menu in Mathematica and then selecting Documentation Center. Or, you can select a function name in any notebook and press F1. Just like variables you can see a function definition by preceding the function with a ?
?Plot
When looking up a function, you can use the * symbol to represent a wildcard:
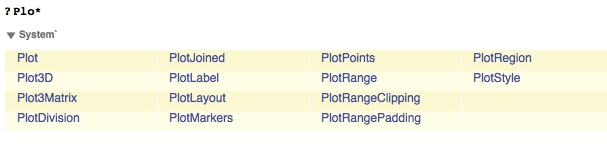
If you type a function and then press CTRL+SHIFT+K or Command+SHIFT+K, Mathematica will show you the parameters that the function takes.
Plot takes one parameter.To plot several functions together, you can put them in a list as the first argument to Plot:
Plot[{Sin[x], 2 Sin[2 x], 1/3 Sin[3 x]}, {x, 0, 2 Π}]
The Plot3D function plots a function as a three-dimensional surface.
Plot3D[Sin[x - Sin[y]], {x, 0, 3 Pi}, {y, 0, 4 Pi}]To zoom, hold down the keys indicated in the table and when the small set of coordinate axes appears at the bottom of your cursor, move your cursor over the graphic and then drag the pointer up to zoom in and down to zoom out.
Use the SHIFT key to pan.
You can combine surfaces:
Plot3D[{Sin[x - Sin[y]], Sin[y - Cos[x]]}, {x, 0, 3 Pi}, {y, 0,
4 Pi}]
Plot3D[{Sin[x - Sin[y]], Sin[y - Cos[x]]}, {x, 0, 3 Pi}, {y, 0,
4 Pi}, PlotStyle -> {Yellow, Cyan}]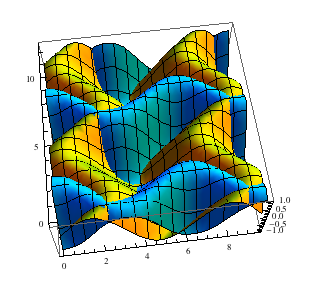
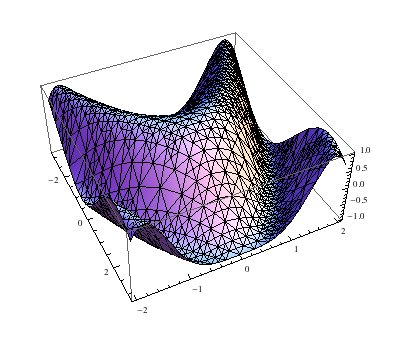
Setting Mesh to All displays all points and lines computed by the plotting functions to construct the graphic. This gives a visualization of the sampling routines of Plot3D.
Plot3D[Cos[x + y^2], {x, -\[Pi], \[Pi]}, {y, -2, 2}, Mesh -> All]
 .
.
You can also use parametric equations:
ParametricPlot3D[{t/5, Sin[t], Cos[t]}, {t, 0, 6 Pi}] RegionPlot3D[
x^2 + y^2 + z^2 > 1 && x + y - z <= 2, {x, -1, 1}, {y, 0, 1}, {z, -1,
1}]
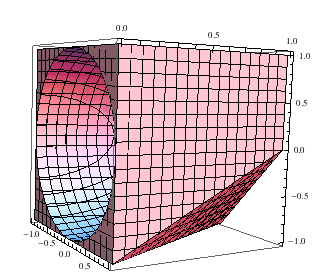
RevolutionPlot3D creates a form that is derived by revolving a curve around the z axis.
RevolutionPlot3D[t^4 - t^2, {t, 0, 1}]
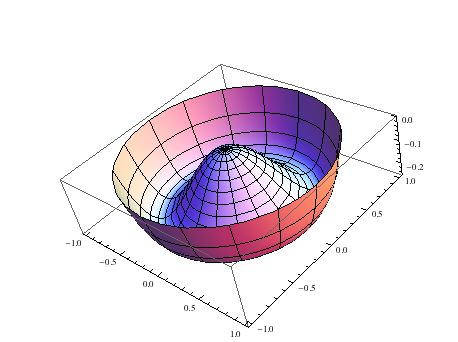
The following is from George Hart's Procedural Generation of Sculptural Forms
Mathematica has a built in Polyhedra library which includes Platonics, Archimedeans, and their duals.The function PolyhedronData[] takes a string and returns that type of polyhedron. It is returned in a form called a graphics complex (GC) which displays as a resizable 3D image that can be rotated by dragging the mouse over it:
PolyhedronData["Dodecahedron"]
vertices[gc_]:= N[gc[[1,1]]]
The N[] function causes the result to be returned in a numeric (floating point) format, without symbolic expressions such as square roots.
The example below uses this function to find the vertices of the built-in cube and observe that it is an axis-aligned unit-edge-length cube centered at the origin. The output, at right, is a list of eight points; each point is a list of the form {x,y,z}.
vertices[PolyhedronData["Cube"]]
{{-0.5,-0.5,-0.5}, {-0.5,-0.5,0.5}, {-0.5,0.5,-0.5}, {-0.5,0.5,0.5},
{0.5,-0.5,-0.5}, {0.5,-0.5,0.5},
{0.5,0.5,-0.5}, {0.5,0.5,0.5}}
faces[gc_] := Map[vertices[gc][[#]]&, gc[[1,2,1]],{2}]
cube = faces[PolyhedronData["Cube"]]
{{{0.5,0.5,0.5},{-0.5,0.5,0.5},{-0.5,-0.5,0.5},{0.5,-0.5,0.5}}, {{0.5,0.5,0.5},{0.5,-0.5,0.5},{0.5,-0.5,-0.5},{0.5,0.5,-0.5}}, {{0.5,0.5,0.5},{0.5,0.5,-0.5},{-0.5,0.5,-0.5},{-0.5,0.5,0.5}}, {{-0.5,0.5,0.5},{-0.5,0.5,-0.5},{-0.5,-0.5,-0.5},{-0.5,-0.5,0.5}}, {{-0.5,-0.5,-0.5},{-0.5,0.5,-0.5},{0.5,0.5,-0.5},{0.5,-0.5,-0.5}}, {{-0.5,-0.5,0.5},{-0.5,-0.5,-0.5},{0.5,-0.5,-0.5},{0.5,-0.5,0.5}}}
view[obj_] := Graphics3D[Map[Polygon,obj], Boxed␣False] view[cube]
Export["cube.stl", view[object]]
Tetrahedron and compounds
To distinguish an object's interior from it's exterior, Rapid Prototyping machines require that vertices of each face be listed in counterclockwise order. A function to create a tetrahedron from a list of four vertices determines this ordering from a single test of aboveness, using Mathematica's If [test, then, else] syntax:
tetra[{p1_,p2_,p3_,p4_}]:= If[above[p1,{p2,p3,p4}], {{p1,p2,p3},{p1,p3,p4},{p1,p4,p2},{p3,p2,p4}},
{{p1,p3,p2},{p1,p4,p3},{p1,p2,p4},{p3,p4,p2}}]v4={{1,1,1},{1,-1,-1},{-1,1,-1},{-1,-1,1}} view[tetra[v4]]view[Join[tetra[v4], tetra[-v4]]]
v=vertices[PolyhedronData["Dodecahedron"]]
view[Join[tetra[{v[[1]],v[[11]],v[[17]],v[[20]]}], tetra[{v[[2]],v[[4]],v[[7]],v[[9]]}],
tetra[{v[[3]],v[[12]],v[[13]],v[[15]]}], tetra[{v[[5]],v[[8]],v[[14]],v[[18]]}], tetra[{v[[6]],v[[10]],v[[16]],v[[19]]}]]]
Transformations: translate, scale, and rotate
You can translate an object by adding a vector offset to each vertex. The syntax used here is a bit cryptic, with Map used to create a list by applying a function to elements of a given list, the & symbol is used to create an anonymous function with # as the argument placeholder, and {2} as a special argument to Map indicating the function is to be applied at level 2 (the xyz points) rather than to the top level elements of the list (the faces). Test the function by creating a cube with another cube translated 1.1 units in the X direction:
translate[obj_, offset_]:= Map[(#+offset)&, obj, {2}]
view[Join[cube, translate[cube,{1.1,0,0}]]]
view[Join[cube, translate[0.5 cube, {0.75,0,0}]]]
view[Apply[Join, Table[translate[i cube,{i^2/2,0,0}], {i,1,10}]]]
rotate[obj_, angle_, axis_] := Map[(RotationMatrix[angle,axis].#)&, obj, {2}]
view[Join[rotate[cube, Pi/4, {1,0,0}],
rotate[cube, Pi/4, {0,1,0}],
rotate[cube, Pi/4, {0,0,1}]]]
Manipulate[view[poke[faces[PolyhedronData["Icosahedron"]], height]], {height,-1,3}]Sierpinski's Triangle
It is not hard to write a program that generates a computer-rendered image of a Sierpinski Tetrahedron, but printing it out would be difficult/impossible because the mathematical points just barely meet. George Hart, artist and mathematician has created an stl file that can be printed
To open it up in Openscad save the openscad file in the same directory as the stl file:
module triangle(){
scale(10)
import_stl("sierpinski5-george-hart.stl");
}
translate ([-8,-14,0])
triangle();
New York State Learning Standards
-
STANDARD 1
Analysis, Inquiry, and Design: MATHEMATICAL ANALYSIS
Key Idea 3: details
Critical thinking skills are used in the solution of mathematical problems.Elementary M3.1 Explore and solve problems generated from school, home, and community situations, using concrete objects or manipulative materials when possible. √ M3.1a Use appropriate scientific tools, such as metric rulers, spring scale, pan balance, graph paper, thermometers [Fahrenheit and Celsius], graduated cylinder to solve problems about the natural world √
Intermediate M3.1 Apply algebraic and geometric concepts and skills to the solution of problems. √ M3.1a Explain the physical relevance of properties of a graphical representation of real-world data, e.g., slope, intercepts, area under the curve
Physics M3.1 Apply mathematical knowledge to solve real-world problems and problems that arise from the investigation of mathematical ideas, using representations such as pictures, charts, and tables. M3.1a Use appropriate scientific tools to solve problems about the natural world √ -
STANDARD 1
Analysis, Inquiry, and Design SCIENTIFIC INQUIRY:
Key Idea 1: details
The central purpose of scientific inquiry is to develop explanations of natural phenomena in a continuing, creative process.Elementary S1.1 Ask "why" questions in attempts to seek greater understanding concerning objects and events they have observed and heard about. S1.1a Observe and discuss objects and events and record observations. √ S1.1b Articulate appropriate questions based on observations. √ S1.2 Question the explanations they hear from others and read about, seeking clarification and comparing them with their own observations and understandings. S1.2a Identify similarities and differences between explanations received from others or in print and personal observations or understandings S1.3 Develop relationships among observations to construct descriptions of objects and events and to form their own tentative explanations of what they have observed. √ S1.3a Clearly express a tentative explanation or description which can be tested.
Intermediate S1.1 Formulate questions independently with the aid of references appropriate for guiding the search for explanations of everyday observations. S1.1a Formulate questions about natural phenomena. S1.1b Identify appropriate references to investigate a question. S1.1c Refine and clarify questions so that they are subject to scientific investigation. S1.2 Construct explanations independently for natural phenomena, especially by proposing preliminary visual models of phenomena. √ S1.2a Independently formulate a hypothesis. √ S1.2b Propose a model of a natural phenomenon. S1.2c Differentiate among observations, inferences, predictions, and explanations S1.3 Represent, present, and defend their proposed explanations of everyday observations so that they can be understood and assessed by others. S1.4 Seek to clarify, to assess critically, and to reconcile with their own thinking the ideas presented by others, including peers, teachers, authors, and scientists. √
Physics S1.1 Develop extended visual models and mathematical formulations to represent an understanding of natural phenomena. S1.2 Clarify ideas through reasoning,research,and discussion. √ S1.3 Evaluate competing explanations and overcome misconceptions. -
STANDARD 1
Analysis, Inquiry, and Design SCIENTIFIC INQUIRY:
Key Idea 2: details
Beyond the use of reasoning and consensus, scientific inquiry involves the testing of proposed explanations involving the use of conventional techniques and procedures and usually requiring considerable ingenuity.Elementary S2.1 Develop written plans for exploring phenomena or for evaluating explanations guided by questions or proposed explanations they have helped formulate. S2.1a Indicate materials to be used and steps to follow to conduct the investigation and describe how data will be recorded (journal, dates and times, etc.) √ S2.2 Share their research plans with others and revise them based on their suggestions. √ S2.2a Explain the steps of a plan to others, actively listening to their suggestions for possible modification of the plan, seeking clarification and understand- ing of the suggestions and modifying the plan where appropriate √ S2.3 Carry out their plans for exploring phenomena through direct observation and through the use of simple instruments that permit measurement of quantities, such as length, mass, volume, temperature, and time. √ S2.3a Use appropriate "inquiry and process skills" to collect data. √ S2.3b Record observations accurately and concisely √
Intermediate S2.1 Use conventional techniques and those of their own design to make further observations and refine their explanations, guided by a need for more information. √ S2.1a Demonstrate appropriate safety techniques. S2.1b Conduct an experiment designed by others. S2.1c Design and conduct an experiment to test a hypothesis. S2.1d Use appropriate tools and conventional techniques to solve problems about the natural world, including: - measuring
- observing
- describing
- classifying
- sequencing
√ S2.2 Develop, present, and defend formal research proposals for testing their own explanations of common phenomena, including ways of obtaining needed observations and ways of conducting simple controlled experiments S2.2a Include appropriate safety procedures. S2.2b Design scientific investigations (e.g., observing, describing, and comparing; collecting samples; seeking more information, conducting a controlled experiment; discovering new objects or phenomena; making models) S2.2c Design a simple controlled experiment. S2.2d Identify independent variables (manipulated), dependent variables (responding), and constants in a simple controlled experiment. S2.2e Choose appropriate sample size and number of trials. S2.3 Carry out their research proposals, recording observations and measurements (e.g., lab notes, audiotape, computer disk, videotape) to help assess the explanation. √ S2.3a Use appropriate safety procedures. S2.3b Conduct a scientific investigation. S2.3c Collect quantitative and qualitative data. √
Physics S2.1 Devise ways of making observations to test proposed explanations. √ S2.1a Design an experiment to investigate the relationship between physical phenomena. S2.2 Refine research ideas through library investigations, including electronic information retrieval and reviews of the literature, and through peer feedback obtained from review and discussion. S2.3 Develop and present proposals including formal hypotheses to test explanations; i.e., predict what should be observed under specific conditions if the explanation is true. S2.4 Carry out a research plan for testing explanations, including selecting and developing techniques, acquiring and building apparatus, and recording observations as necessary. (Note: This could apply to many activities from simple investigations to long-term projects.) √ -
STANDARD 1
Analysis, Inquiry, and Design: ENGINEERING DESIGN
Key Idea 1: details
Engineering design is an iterative process involving modeling and optimization (finding the best solution within given constraints); this process is used to develop technological solutions to problems within given constraints. (Note: The design process could apply to activities from simple investigations to long-term projects.)Elementary 1.1 Describe objects, imaginary or real, that might be modeled or made differently and suggest ways in which the objects can be changed, fixed, or improved √ 1.2 Investigate prior solutions and ideas from books, magazines, family, friends, neighbors, and community members √ 1.3 Generate ideas for possible solutions, individually and through group activity; apply age-appropriate mathematics and science skills; evaluate the ideas and determine the best solution; and explain reasons for the choices √ 1.4 Plan and build, under supervision, a model of the solution using familiar materials, processes, and hand tools √ 1.5 Discuss how best to test the solution; perform the test under teacher supervision; record and portray results through numerical and graphic means; discuss orally why things worked or didn't work; and summarize results in writing, suggesting ways to make the solution better √
Intermediate T1.1 Identify needs and opportunities for technical solutions from an investigation of situations of general or social interest. T1.1a Identify a scientific or human need that is subject to a technological solution which applies scientific principles √ T1.2 Locate and utilize a range of printed, electronic, and human information resources to obtain ideas. √ T1.2a Use all available information systems for a preliminary search that addresses the need. √ T1.3 Consider constraints and generate several ideas for alternative solutions, using group and individual ideation techniques (group discussion, brainstorming, forced connections, role play); defer judgment until a number of ideas have been generated; evaluate (critique) ideas; and explain why the chosen solution is optimal. √ T1.3a Generate ideas for alternative solutions √ T1.3b Evaluate alternatives based on the constraints of design. √ T1.4 Develop plans, including drawings with measurements and details of construction, and construct a model of the solution, exhibiting a degree of craftsmanship. √ T1.4a Design and construct a model of the product or process √ T1.4b Construct a model of the product or process √ T1.5 In a group setting, test their solution against design specifications, present and evaluate results, describe how the solution might have been modified for different or better results, and discuss trade-offs that might have to be made. √ T1.5a Test a design √ T1.5b Evaluate a design √
Commencement 1.1 Initiate and carry out a thorough investigation of an unfamiliar situation and identify needs and opportunities for technological invention or innovation. 1.2 Identify, locate, and use a wide range of information resources including subject experts, library references, magazines, videotapes, films, electronic data bases and online services, and discuss and document through notes and sketches how findings relate to the problem √ 1.3 Generate creative solution ideas, break ideas into the significant functional elements, and explore possible refinements; predict possible outcomes using mathematical and functional modeling techniques; choose the optimal solution to the problem, clearly documenting ideas against design criteria and constraints; and explain how human values, economics, ergonomics, and environmental considerations have influenced the solution √ 1.4 Develop work schedules and plans which include optimal use and cost of materials, processes, time, and expertise; construct a model of the solution, incorporating developmental modifications while working to a high degree of quality (craftsmanship) √ 1.5 In a group setting, devise a test of the solution relative to the design criteria and perform the test; record, portray, and logically evaluate performance test results through quanitative, graphic, and verbal means; and use a variety of creative verbal and graphic techniques effectively and persuasively to present conclusions, predict impacts and new problems, and suggest and pursue modifications √ -
STANDARD 2
INFORMATION SYSTEMS
Key Idea 1: details
Information technology is used to retrieve, process, and communicate information as a tool to enhance learning.Elementary 1.1 Use computer technology,traditional paper-based resources,and interpersonal discussions to learn, do, and share science in the classroom √ 1.2 Select appropriate hardware and software that aids in word-processing, creating databases, telecommunications, graphing, data display, and other tasks √ 1.3 Use information technology to link the classroom to world events.
Intermediate 1.1 Use a range of equipment and software to integrate several forms of information in order to create good-quality audio, video, graphic, and text-based presentations. √ 1.2 Use spreadsheets and database software to collect, process, display, and analyze information. Students access needed information from electronic databases and on-line telecommunication services. 1.3 Systematically obtain accurate and relevant information pertaining to a particular topic from a range of sources, including local and national media, libraries, muse- ums, governmental agencies, industries, and individuals. √ 1.4 Collect data from probes to measure events and phenomena. 1.4a Collect the data, using the appropriate, available tool. √ 1.4b Organize the data. 1.4c Use the collected data to communicate a scientific concept √ 1.5 Use simple modeling programs to make predictions. √
Physics 1.1 Understand and use the more advanced features of word processing, spreadsheets, and database software. √ 1.2 Prepare multimedia presentations demonstrating a clear sense of audience and purpose. (Note: Multimedia may include posters, slides, images, presentation software, etc.) √ 1.2a Extend knowledge of physical phenomena through independent investigation, e.g., literature review, electronic resources, library research 1.2b Use appropriate technology to gather experimental data, develop models,and present results. √ 1.3 Access, select, collate, and analyze information obtained from a wide range of sources such as research databases, foundations, organizations, national libraries, and electronic communication networks, including the Internet. √ 1.3a Use knowledge of physics to evaluate articles in the popular press on contemporary scientific topics. 1.4 Utilize electronic networks to share information. √ 1.5 Model solutions to a range of problems in mathematics, science, and technology, using computer simulation software. √ 1.5a Use software to model and extend classroom and laboratory experiences,recognizing the differences between the model used for understanding and real-world behavior √ -
STANDARD 2
INFORMATION SYSTEMS:
Key Idea 2: details
Knowledge of the impacts and limitations of information systems is essential to its effective and ethical use.Elementary 2.1 Use a variety of media to access scientific information 2.2 Consult several sources of information and points of view before drawing conclusions √ 2.3 Identify and report sources in oral and written communications √
Intermediate 2.1 Understand the need to question the accuracy of information displayed on a computer because the results produced by a computer may be affected by incorrect data entry. 2.1a Critically analyze data to exclude erroneous information 2.1b Identify and explain sources of error in a data collection 2.2 Understand the need to question the accuracy of information displayed on a computer because the results produced by a computer may be affected by incorrect data entry. 2.2a Critically analyze data to exclude erroneous information 2.2b Identify advantages and limitations of data-handling programs and graphics programs. √ 2.3 Understand why electronically stored personal information has greater potential for misuse than records kept in conventional form.
-
STANDARD 5
Technology: Engineering Design
Key Idea 1: details
(same as STANDARD 1 Analysis, Inquiry, and Design: ENGINEERING DESIGN)
Engineering design is an iterative process involving modeling and optimization used to develop technological solutions to problems within given constraints.Elementary T1.1 Describe objects, imaginary or real, that might be modeled or made differently and suggest ways in which the objects can be changed, fixed, or improved. √ T1.2 Investigate prior solutions and ideas from books, magazines, family, friends, neighbors, and community members. √ T1.3 Generate ideas for possible solutions, individually and through group activity; apply age-appropriate mathemat- ics and science skills; evaluate the ideas and determine the best solution; and explain reasons for the choices. √ T1.4 Plan and build, under supervision, a model of the solution using familiar materials, processes, and hand tools √ T1.5 Discuss how best to test the solution; perform the test under teacher supervision; record and portray results through numerical and graphic means; discuss orally why things worked or didn't work; and summarize results in writing, suggesting ways to make the solution better. √
Intermediate T1.1 Identify needs and opportunities for technical solutions from an investigation of situations of general or social interest. T1.2 Locate and utilize a range of printed, electronic, and human information resources to obtain ideas. √ T1.3 Consider constraints and generate several ideas for alternative solutions, using group and individual ideation techniques (group discussion, brainstorming, forced connections, role play); defer judgment until a number of ideas have been generated; evaluate (critique) ideas; and explain why the chosen solution is optimal. √ T1.4 Develop plans, including drawings with measurements and details of construction, and construct a model of the solution, exhibiting a degree of craftsmanship. √ T1.5 In a group setting, test their solution against design specifications, present and evaluate results, describe how the solution might have been modified for different or better results, and discuss tradeoffs that might have to be made. √
Commencement T1.1 Initiate and carry out a thorough investigation of an unfamiliar situation and identify needs and opportunities for technological invention or innovation. T1.2 Identify, locate, and use a wide range of information resources including subject experts, library references, magazines, videotapes, films, electronic data bases and on-line services, and discuss and document through notes and sketches how findings relate to the problem. √ T1.3 Generate creative solution ideas, break ideas into the significant functional elements, and explore possible refinements; predict possible outcomes using mathematical and functional modeling techniques; choose the optimal solution to the problem, clearly documenting ideas against design criteria and constraints; and explain how human values, economics, ergonomics, and environmental considerations have influenced the solution. √ T1.4 Develop work schedules and plans which include optimal use and cost of materials, processes, time, and expertise; construct a model of the solution, incorporating developmental modifications while working to a high degree of quality (craftsmanship). √ T1.5 In a group setting, devise a test of the solution relative to the design criteria and perform the test; record, portray, and logically evaluate performance test results through quantitative, graphic, and verbal means; and use a vari- ety of creative verbal and graphic techniques effectively and persuasively to present conclusions, predict impacts and new problems, and suggest and pursue modifications. √ -
STANDARD 5
Technology: Engineering Design
Key Idea 2: details
Technological tools, materials, and other resources should be selected on the basis of safety, cost, availability, appropriateness, and environmental impact; technological processes change energy, information, and material resources into more useful forms.Elementary 2.1 Explore, use, and process a variety of materials and energy sources to design and construct things. √ 2.2 Understand the importance of safety, cost, ease of use, and availability in selecting tools and resources for a specific purpose. 2.3 Develop basic skill in the use of hand tools 2.4 Use simple manufacturing processes (e.g., assembly, multiple stages of production, quality control) to produce a product √ 2.5 Use appropriate graphic and electronic tools and techniques to process information. √
Intermediate 2.1 Choose and use resources for a particular purpose based upon an analysis and understanding of their properties, costs, availability, and environmental impact √ 2.2 Use a variety of hand tools and machines to change materials into new forms through forming, separating, and combining processes, and processes which cause internal change to occur √ 2.3 Combine manufacturing processes with other technological processes to produce, market, and distribute a product 2.4 Process energy into other forms and information into more meaningful information.
Commencement 2.1 Test, use, and describe the attributes of a range of material (including synthetic and composite materials), information, and energy resources √ 2.2 Select appropriate tools, instruments, and equipment and use them correctly to process materials, energy, and information √ 2.3 Explain tradeoffs made in selecting alternative resources in terms of safety, cost, properties, availability, ease of processing, and disposability 2.4 Describe and model methods (including computer-based methods) to control system processes and monitor system outputs √ -
STANDARD 5
Technology: Computer Technology
Key Idea 3: details
Computers, as tools for design, modeling, information processing, communication, and system control, have greatly increased human productivity and knowledge.Elementary 3.1 Identify and describe the function of the major components of a computer system. 3.2 Use the computer as a tool for generating and drawing ideas. √ 3.3 Control computerized devices and systems through programming. √ 3.4 Model and simulate the design of a complex environment by giving direct commands. √
Intermediate 3.1 Assemble a computer system including keyboard, central processing unit and disc drives, mouse, modem, printer, and monitor 3.2 Use a computer system to connect to and access needed information from various Internet sites √ 3.3 Use computer hardware and software to draw and dimension prototypical designs √ 3.4 Use a computer as a modeling tool √ 3.5 Use a computer system to monitor and control external events and/or systems √
Commencement 3.1 Understand basic computer architecture and describe the function of computer subsystems and peripheral devices 3.2 Select a computer system that meets personal needs 3.3 Attach a modem to a computer system and telephone line, set up and use communications software, connect to various online networks, including the Internet, and access needed information using email, telnet, gopher, ftp, and web searches √ 3.4 Use computer-aided drawing and design (CADD) software to model realistic solutions to design problems √ 3.5 Develop an understanding of computer programming and attain some facility in writing computer programs √ -
STANDARD 5
Technology: Management of Technology
Key Idea 7: details
Project management is essential to ensuring that technological endeavors are profitable and that products and systems are of high quality and built safely, on schedule, and within budget.Elementary 7.1 Participate in small group projects and in structured group tasks requiring planning, financing, production, quality control, and follow-up. √ 7.2 Speculate on and model possible technological solutions that can improve the safety and quality of the school or community environment.
Intermediate 7.1 Manage time and financial resources in a technological project √ 7.2 Provide examples of products that are well (and poorly) designed and made, describe their positive and negative attributes, and suggest measures that can be implemented to monitor quality during production 7.3 Assume leadership responsibilities within a structured group activity √
Commencement 7.1 Develop and use computer-based scheduling and project tracking tools, such as flow charts and graphs 7.2 Explain how statistical process control helps to assure high quality output 7.3 Discuss the role technology has played in the operation of successful U.S. businesses and under what circumstance they are competitive with other countries 7.4 Explain how technological inventions and innovations stimulate economic competitiveness and how, in order for an innovation to lead to commercial success, it must be translated into products and services with marketplace demand 7.5 Describe new management techniques (e.g., computer-aided engineering, computer-integrated manufacturing, total quality management, just-in-time manufacturing), incorporate some of these in a technological endeavor, and explain how they have reduced the length of design-to-manufacture cycles, resulted in more flexible factories, and improved quality and customer satisfaction 7.6 Help to manage a group engaged in planning, designing, implementation, and evaluation of a project to gain understanding of the management dynamics √ -
STANDARD 6
Interconnectedness: Common Themes MODELS:
Key Idea 2: details
Models are simplified representations of objects, structures, or systems used in analysis, explanation, interpretation, or design.Elementary 2.1 Analyze,construct,and operate models in order to discover attributes of the real thing √ 2.2 Discover that a model of something is different from the real thing but can be used to study the real thing √ 2.3 Use different types of models, such as graphs,sketches,diagrams,and maps,to represent various aspects of the real world
Intermediate 2.1 Select an appropriate model to begin the search for answers or solutions to a question or problem. 2.2 Use models to study processes that cannot be studied directly (e.g., when the real process is too slow, too fast, or too dangerous for direct observation). √ 2.3 Demonstrate the effectiveness of different models to represent the same thing and the same model to represent different things.
Physics 2.1 Revise a model to create a more complete or improved representation of the system. 2.2 Collect information about the behavior of a system and use modeling tools to represent the operation of the system. √ 2.2a Use observations of the behavior of a system to develop a model 2.3 Find and use mathematical models that behave in the same manner as the processes under investigation. 2.3a Represent the behavior of real-world systems,using physical and mathematical models √ 2.4 Compare predictions to actual observations, using test models. √ 2.4a Validate or reject a model based on collated experimental data √ 2.4b Predict the behavior of a system,using a model √ -
STANDARD 6
Interconnectedness: Common Themes OPTIMIZATION:
Key Idea 6: details
In order to arrive at the best solution that meets criteria within constraints, it is often necessary to make trade-offs.Elementary 6.1 Choose the best alternative of a set of solutions under given constraints. √ 6.2 Explain the criteria used in selecting a solution orally and in writing √
Intermediate 6.1 Determine the criteria and constraints and make trade-offs to determine the best decision. √ 6.2 Use graphs of information for a decision-making problem to determine the optimum solution.
Physics Determine optimal solutions to problems that can be solved using quantitative methods √ -
STANDARD 7
Interdisciplinary Problem Solving STRATEGIES:
Key Idea 2: details
Solving interdisciplinary problems involves a variety of skills and strategies, including effective work habits; gathering and processing information; generating and analyzing ideas; realizing ideas; making connections among the common themes of mathematics, science, and technology; and presenting results.Physics 2.1 Collect,analyze,interpret,and present data,using appropriate tools √ 2.2 When students participate in an extended,culminating mathematics,science,and technology project, then students should: Work effectively—Contributing to the work of a brainstorming group, laboratory partnership, cooperative learning group, or project team; planning procedures; identify and managing responsibilities of team members; and staying on task, whether working alone or as part of a group. √ Gather and process information —Accessing information from printed media, electronic data bases, and community resources and using the information to develop a definition of the problem and to research possible solutions. √ Generate and analyze ideas — Developing ideas for proposed solutions, investigating ideas, collecting data, and showing relationships and patterns in the data. √ Observe common themes—Observing examples of common unifying themes, applying them to the problem, and using them to better understand the dimensions of the problem. √ Realize ideas—Constructing components or models, arriving at a solution, and evaluating the result. √ Present results—Using a variety of media to present the solution and to communicate the results. √
CDOS
- Standard 2: Integrated Learning details
Students will demonstrate how academic knowledge and skills are applied in the workplace and other settings.
Integrated learning encourages students to use essential academic concepts, facts, and procedures in applications related to life skills and the world of work. This approach allows students to see the usefulness of the concepts that they are being asked to learn and to understand their potential application in the world of work.
Elementary 2.1 Identify academic knowledge and skills that are required in specific occupations 2.2 Demonstrate the difference between the knowledge of a skill and the ability to use the skill 2.3 Solve problems that call for applying academic knowledge and skills. √
Intermediate 2.1 Apply academic knowledge and skills using an interdisciplinary approach to demonstrate the relevance of how these skills are applied in work-related situations in local, state, national, and international communities 2.2 Solve problems that call for applying academic knowledge and skills √ 2.3 Use academic knowledge and skills in an occupational context, and demonstrate the application of these skills by using a variety of communication techniques (e.g., sign language, pictures, videos, reports, and technology).
Commencement 2.1 Demonstrate the integration and application of academic and occupational skills in their school learning, work, and personal lives. √ 2.2 Use academic knowledge and skills in an occupational context, and demonstrate the application of these skills by using a variety of communication techniques (e.g., sign language, pictures, videos, reports, and technology) √ 2.3 Research, interpret, analyze, and evaluate information and experiences as related to academic knowledge and technical skills when completing a career plan. - Standard 3a: Universal Foundation Skills details
Students will demonstrate mastery of the foundation skills and competencies essential for success in the workplace.
- Basic skills
Basic skills include the ability to read, write, listen, and speak as well as perform arithmetical and mathematical functions.
Elementary 3.1.1 Listen to and read the ideas of others and express themselves both orally and in writing; they use basic mathematical concepts and computations to solve problems. √
Intermediate 3.1.1 Listen to and read the ideas of others and analyze what they hear and read; acquire and use information from a variety of sources; and apply a combination of mathematical operations to solve problems in oral or written form. √
Commencement 3.1.1 Use a combination of techniques to read or listen to complex information and analyze what they hear or read; convey information confidently and coherently in written or oral form; and analyze and solve mathematical problems requiring use of multiple computational skills. √ - Thinking skills
Thinking skills lead to problem solving, experimenting, and focused observation and allow the application of knowledge to new and unfamiliar situations.
Elementary 3.2.1 Use ideas and information to make decisions and solve problems related to accomplishing a task. √
Intermediate 3.2.1 Evaluate facts, solve advanced problems, and make decisions by applying logic and reasoning skills. √
Commencement 3.2.1 Demonstrate the ability to organize and process information and apply skills in new ways. √
- Personal Qualities
Personal qualities generally include competence in self-management and the ability to plan, organize, and take independent action.
Elementary 3.3.1 Demonstrate the personal qualities that lead to responsible behavior. √
Intermediate 3.3.1 Demonstrate the ability to work with others, present facts that support arguments, listen to dissenting points of view, and reach a shared decision. √
Commencement 3.3.1 Demonstrate leadership skills in setting goals, monitoring progress, and improving their performance. √
- Interpersonal Skills
Positive interpersonal qualities lead to teamwork and cooperation in large and small groups in family, social, and work situations.
Elementary 3.4.1 Relate to people of different ages and from diverse backgrounds.
Intermediate 3.4.1 Demonstrate the ability to work with others, present facts that support arguments, listen to dissenting points of view, and reach a shared decision. √
Commencement 3.4.1 Communicate effectively and help others to learn a new skill. √
- Technology
Technology is the process and product of human skill and ingenuity in designing and creating things from available resources to satisfy personal and societal needs and wants.
Elementary 3.5.1 Demonstrate an awareness of the different types of technology available to them and of how technology affects society.
Intermediate 3.5.1 Select and use appropriate technology to complete a task. √
Commencement 3.5.1 Apply their knowledge of technology to identify and solve problems. √
- Managing Information
Information management focuses on the ability to access and use information obtained from other people, community resources, and computer networks.Elementary 3.6.1 Describe the need for data and obtain data to make decisions. √
Intermediate 3.6.1 Select and communicate information in an appropriate format (e.g., oral, written, graphic, pictorial, multimedia). √
Commencement 3.6.1 Use technology to acquire, organize, and communicate information by entering, modifying, retrieving, and storing data. √
- Managing Resources
Using resources includes the application of financial and human factors, and the elements of time and materials to successfully carry out a planned activity.Elementary 3.7.1 Demonstrate an awareness of the knowledge, skills, abilities, and resources needed to complete a task. √
Intermediate 3.7.1 Understand the material, human, and financial resources needed to accomplish tasks and activities. √
Commencement 3.7.1 Allocate resources to complete a task. √
- Systems
Systems skills include the understanding of and ability to work within natural and constructed systems.Elementary 3.8.1 Demonstrate understanding of how a system operates and identify where to obtain information and resources within the system. √
Intermediate 3.8.1 Understand the process of evaluating and modifying systems within an organization. √
Commencement 3.8.1 Demonstrate an understanding of how systems performance relates to the goals, resources, and functions of an organization. √
- Basic skills
