Navigation

Introduction
Sketchup
Mathematica
NYS Standards

Polyhedra

Introduction

In elementary geometry a polyhedron (plural polyhedra or polyhedrons) is a geometric solid in three dimensions with flat faces and straight edges.

A polyhedron is made up of a finite number of polygonal faces which are parts of planes; the faces meet in pairs along edges which are straight-line segments, and the edges meet in points called vertices. Cubes, prisms and pyramids are examples of polyhedra. The polyhedron surrounds a bounded volume in three-dimensional space; sometimes this interior volume is considered to be part of the polyhedron, sometimes only the surface is considered, and occasionally only the skeleton of edges.

Many polyhedra are symmetrical. When a polyhedral name is given, such as icosidodecahedron, the most symmetrical geometry is almost always implied.

Some of the most common names in particular are often used with regular in front or implied because for each there are different types which have little in common except for having the same number of faces. The common polyhedra are the
  • triangular pyramid or tetrahedron (4 triangles)
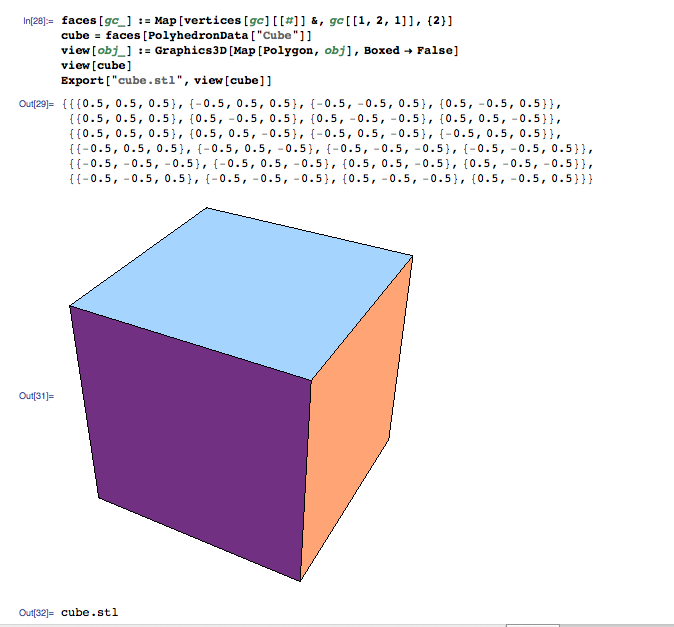
  • the cube or hexahedron (6 squares)
  • the octahedron (8 triangles)
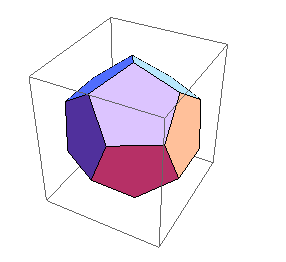
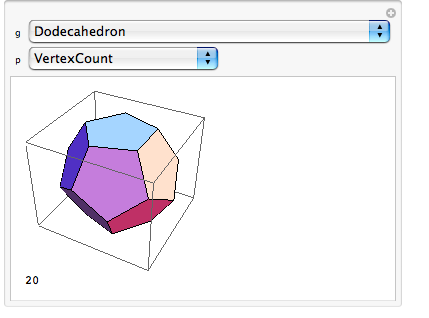
  • the dodecahedron (12 pentagons)
  • the icosahedron (20 triangles)


Archimedean solids consist of two or three different shapes. A cuboctahedron, a truncated tetrahedron and a truncated octahedron are examples of Archimedean solids.

www.korthalsaltes.com is a fantastic resource for paper models.


Vertex Generator

IMG_3362_preview_medium.jpg

Here is the openscad script to create the vertices: 
//===================================== 
// This is public Domain Code
// Contributed by: Sjoerd de Jong (@ssured)
// June 2011
//=====================================

/*
 This is a script to print vertex connectors for creating solid models
 Parameters for all platonic solids, archimedean solids, prisms and antiprisms are included
 It's also possible to model your own custom connectors, to build whatever you like
 You can even model a .stl file in real space, by printing all vertices... Have fun!
 
 see http://en.wikipedia.org/wiki/Uniform_polyhedron
 see http://en.wikipedia.org/wiki/Archimedean_solid
 see http://en.wikipedia.org/wiki/Platonic_solid
*/

// PARAMETERS YOU SHOULD CHANGE, all in mm
diameter = 6;
thickness = diameter/2;
length = 2*diameter;

// cylinder hole precision
// based on http://hydraraptor.blogspot.com/2011/02/polyholes.html
$fn = max(round(diameter*2),3);

//For a polyhedron:
//=====================================================================
//supply the name:
vertex(polyhedrondata[   snubcube  ]);

//For a prism / antiprism with n-face base, print 2n vertices (n>=2):
//=====================================================================
//vertex(prism(5));
//vertex(antiprism(2));

//For a n-sided polygon / dihedron, print n vertices
//=====================================================================
//vertex(polygon(5));
//vertex(dihedron(3));

//For a custom vertex, based on supplied vectors:
//=====================================================================
//determine number of edges coming in, supply vectors for all outgoing edges
//vertex(custom3([1,1,1],[-1,1,1],[1,-1,1]));
//vertex(custom4([1,1,5],[-1,1,5],[1,-1,5],[-1,-1,5]));

//For a full custom
//=====================================================================
//module syntax:
//module vertex([normal, offset, [vectors]]);
// - normal: defines the direction perpendicular to the face of the vertex connector
//     when [0,0,0] is used, a normal from [offset]->[0,0,0] is used, also a hole is added in this direction
// - offset: offset of the base for vectors, for ease of building a connector not centered at [0,0,0]
// - [vectors]: vectors for all outgoing edges from this connector




// =====================================================================
// SCAD MODELING STARTS FROM HERE
// Constants
m=0.0;
radius = diameter / 2; // for convenience
tau = (1 + sqrt(5)) / 2; // golden ratio, used a lot
xi = (pow(17+3*sqrt(33),1/3)-pow(-17+3*sqrt(33),1/3)-1)/3; // used for snub cube
xis = pow(tau/2+0.5*sqrt(tau-5/27),1/3)+pow(tau/2-0.5*sqrt(tau-5/27),1/3); // used for snub dodecahedron
alpha = xis - 1/xis; // used for snub dodecahedron
beta = xis*tau+tau*tau+tau/xis; // used for snub dodecahedron

// Polyhederon definitions:
// platonic solid
tetrahedron                = 0; // print 4
cube                       = 1; // print 8
octahedron                 = 2; // print 6
dodecahedron               = 3; // print 20
icosahedron                = 4; // print 12

// archimedean solids
truncatedtetrahedron       = 5; // print 12
cuboctahedron              = 6; // print 12
truncatedcube              = 7; // print 24
truncatedoctahedron        = 8; // print 24
rhombicuboctahedron        = 9; // print 24
truncatedcuboctahedron     = 10; // print 48
snubcube                   = 11; // print 24
icosidodecahedron          = 12; // print 30
truncateddodecahedron      = 13; // print 60
truncatedicosahedron       = 14; // print 60
rhombicosidodecahedron     = 15; // print 60
truncatedicosidodecahedron = 16; // print 120
snubdodecahedron           = 17; // print 60

polyhedrondata = [
[/*tetrahedron*/[0,0,0],   [ 1 ,1, 1], [[1,-1,-1], [-1,1,-1], [-1,-1,1]] , 3, [3,3,3]],
[/*cube*/[0,0,0],          [-1,-1,-1], [[1,-1,-1], [-1,1,-1], [-1,-1,1]] , 3, [4,4,4]],
[/*octahedron*/[0,0,0],    [ 0, 0,-1], [[1,0,0],[0,1,0],[-1,0,0],[0,-1,0]], 4, [3,3,3,3]],
[/*dodecahedron*/[0,0,0],  [ 1, 1, 1], [[0,1/tau,tau],[1/tau,tau,0],[tau,0,1/tau]], 3, [5,5,5]],
[/*icosahedron*/[0,0,0],   [0,1,-tau], [[0,-1,-tau],[-tau,0,-1],[-1,tau,0],[1,tau,0],[tau,0,-1]], 5, [3,3,3,3,3]],
[/*truncatedtetrahedron*/[0,0,0], [-3, -1, 1], [[-3, 1, -1],[-1,-3,1], [-1, -1, 3]], 3, [6,3,6]],
[/*cuboctahedron*/[0,0,0],  [1,0,-1], [[0,-1,-1],[0,1,-1],[1,1,0],[1,-1,0]], 4, [4,3,4,3]],
[/*truncatedcube*/[0,0,0],  [1,1,-sqrt(2)+1], [[1,1,sqrt(2)-1],[sqrt(2)-1,1,-1],[1,sqrt(2)-1,-1]], 3, [8,3,8]],
[/*truncatedoctahedron*/[0,0,0], [0,1,-2], [[1,0,-2],[-1,0,-2],[0,2,-1]], 3, [4,6,6]],
[/*rhombicuboctahedron*/[0,0,0], [1,-1,-1-sqrt(2)], [[-1,-1,-1-sqrt(2)],[1,1,-1-sqrt(2)],[1+sqrt(2),-1,-1],[1,-1-sqrt(2),-1]], 4, [4,4,3,4]],
[/*truncatedcuboctahedron*/[0,0,0], [1+sqrt(2),1,-1-sqrt(8)], [[1+sqrt(2),-1,-1-sqrt(8)],[1,1+sqrt(2),-1-sqrt(8)],[1+sqrt(8),1,-1-sqrt(2)]], 3, [8,6,4]],
[/*snubcube*/[0,0,0], [1,-xi,-1/xi], [[-xi,-1,-1/xi],[xi,1,-1/xi],[1/xi,xi,-1],[1/xi,-1,-xi],[xi,-1/xi,-1]], 5, [4,3,3,3,3]],
[/*icosidodecahedron*/[0,0,0], [0,0,-tau], [[0.5,tau/2,-(1+tau)/2],[-0.5,tau/2,-(1+tau)/2],[-0.5,-tau/2,-(1+tau)/2],[0.5,-tau/2,-(1+tau)/2]], 4, [3,5,3,5]],
[/*truncateddodecahedron*/[0,0,0], [0,1/tau,2+tau], [[0,-1/tau,2+tau],[1/tau,tau,2*tau],[-1/tau,tau,2*tau]], 3, [10,3,10]],
[/*truncatedicosahedron*/[0,0,0], [0,1,3*tau], [[0,-1,3*tau],[-tau,2,1+2*tau],[tau,2,1+2*tau]], 3, [6,5,6]],
[/*rhombicosidodecahedron*/[0,0,0], [1,-1,pow(tau,3)], [[-1,-1,pow(tau,3)],[1,1,pow(tau,3)],[tau*tau,-tau,2*tau],[0,-tau*tau,2+tau]], 4, [4,5,4,3]],
[/*truncatedicosidodecahedron*/[0,0,0], [1/tau,1/tau,3+tau], [[-1/tau,1/tau,3+tau],[1/tau,-1/tau,3+tau],[2/tau,tau,2*tau+1]], 3, [4,10,6]],
[/*snubdodecahedron*/[0,0,0], [2*alpha,-2,2*beta], [[-2*alpha,2,2*beta],[(alpha+beta/tau-tau),-(alpha*tau-beta+1/tau),alpha/tau+beta*tau+1],[(alpha+beta/tau+tau),-(-alpha*tau+beta+1/tau),alpha/tau+beta*tau-1],[-alpha+beta/tau-tau,-(alpha*tau+beta-1/tau),-alpha/tau+beta*tau+1],[-(alpha+beta/tau-tau),(alpha*tau-beta+1/tau),alpha/tau+beta*tau+1]], 5, [3,5,3,3,3]]
];

// Prism definitions
function prismcoord(n,k,z) = [cos(k*360/n)/(2*sin(180/n)),sin(k*360/n)/(2*sin(180/n)),z];
function prism(n) = [[0,0,0],prismcoord(n,0,0.5),[prismcoord(n,0,-0.5),prismcoord(n,1,0.5),prismcoord(n,n-1,0.5)],3,[4,n,4]];

// Antiprism definitions
function antiprismcoord(n,k) = [cos(k*180/n),sin(k*180/n),pow(-1,k)*sqrt(0.5*(cos(180/n)-cos(360/n)))];
function antiprism(n) = [[0,0,0],antiprismcoord(n,0),[antiprismcoord(n,1),antiprismcoord(n,2),antiprismcoord(n,2*n-2),antiprismcoord(n,2*n-1)],4,[3,n,3,3]];

// Polygon definition (dihedron)
function dihedron(n) = [[0,0,0],prismcoord(n,0,0),[prismcoord(n,1,0),prismcoord(n,n-1,0)],2,[n,n]];
function polygon(n) = dihedron(n);

// custom connector functions
function custom3(v1,v2,v3) = [CenterOfGravity3(v1,v2,v3),[0,0,0],[v1,v2,v3]];
function custom4(v1,v2,v3,v4) = [CenterOfGravity4(v1,v2,v3,v4),[0,0,0],[v1,v2,v3,v4]];
function custom5(v1,v2,v3,v4,v5) = [CenterOfGravity5(v1,v2,v3,v4,v5),[0,0,0],[v1,v2,v3,v4,v5]];
function custom6(v1,v2,v3,v4,v5,v6) = [CenterOfGravity6(v1,v2,v3,v4,v5,v6),[0,0,0],[v1,v2,v3,v4,v5,v6]];

// TESTING
// Assert all supplied angles and functions are correct
// Done by computing internal angles, and comparing these to expected regular polygon angles
function polyangle(n) = 180-360/n;
module assert(params)
{
	name = params[0];
	origin = params[1];
	endpoints = params[2];
	numpoints = params[3];
	expectedpolygons = params[4];
	if (numpoints > 0){
		// echo("Asserting",pindex,name);
		for (i = [0:numpoints-1]){
			if(abs(VANG(VSUB(endpoints[i],origin),VSUB(endpoints[(i+1==numpoints)?0:i+1],origin))-polyangle(expectedpolygons[i]))>0.01) {
				echo("FAIL:",name," i ",i," poly ",expectedpolygons[i]," exp angle ",polyangle(expectedpolygons[i])," - found:",VANG(VSUB(endpoints[i],origin),VSUB(endpoints[(i+1==numpoints)?0:i+1],origin)));
			}
		}
	}
}
for (assertionindex = [0:snubdodecahedron]){
	assert(polyhedrondata[assertionindex]);
	if (assertionindex > 1){
		assert(prism(assertionindex));
		assert(antiprism(assertionindex));
		assert(dihedron(assertionindex));
	}
}

// VECTOR MATH FUNCTIONS, from http://www.thingiverse.com/thing:9447
// Made by William A Adams

function VSUM(v1, v2) = [v1[0]+v2[0], v1[1]+v2[1], v1[2]+v2[2]];
function VSUB(v1, v2) = [v1[0]-v2[0], v1[1]-v2[1], v1[2]-v2[2]];
function VMULT(v1, v2) = [v1[0]*v2[0], v1[1]*v2[1], v1[2]*v2[2]];

// Magnitude of a vector
// Gives the Euclidean norm
function VLENSQR(v) = (v[0]*v[0]+v[1]*v[1]+v[2]*v[2]);
function VLEN(v) = sqrt(VLENSQR(v));
function VMAG(v) = sqrt(v[0]*v[0]+v[1]*v[1]+v[2]*v[2]);

// Returns the unit vector associated with a vector
function VUNIT(v) = v/VMAG(v);
function VNORM(v) = v/VMAG(v);

// The scalar, or 'dot' product
// law of cosines
// if VDOT(v1,v2) == 0, they are perpendicular
function SPROD(v1,v2) = v1[0]*v2[0]+v1[1]*v2[1]+v1[2]*v2[2];
function VDOT(v1v2) = SPROD(v1v2[0], v1v2[1]);

// The vector, or Cross product
// Given an array that contains two vectors
function VPROD(vs) = [
	(vs[0][1]*vs[1][2])-(vs[1][1]*vs[0][2]), 
	(vs[0][2]*vs[1][0])-(vs[1][2]*vs[0][0]),
	(vs[0][0]*vs[1][1])-(vs[1][0]*vs[0][1])];
function VCROSS(v1, v2) = VPROD([v1,v2]);

// Calculate the angle between two vectors
function VANG(v1, v2) = acos(VDOT([v1,v2])/(VMAG(v1)*VMAG(v2)));

// Calculate the signed angle between two vectors, seen from normal n
// source: http://tomyeah.com/signed-angle-between-two-vectors3d-in-cc/
function VSANG(v1, v2, n) = atan2(SPROD(VNORM(n),VCROSS(VNORM(v1),VNORM(v2))),SPROD(VNORM(v1),VNORM(v2)));

// returns a semi random vector perpendicular to the original vector
function VPERP(v) = [v[1], -v[0], 0];
// inverts a vector
function VINV(v) = [-v[0], -v[1], -v[2]];

function AvgThree(v1,v2,v3) = (v1+v2+v3)/3; 
function AvgFour(v1,v2,v3,v4) = (v1+v2+v3+v4)/4;
function AvgFive(v1,v2,v3,v4,v5) = (v1+v2+v3+v4+v5)/5;
function AvgSix(v1,v2,v3,v4,v5,v6) = (v1+v2+v3+v4+v5+v6)/6;

function CenterOfGravity3(p0, p1, p2) = [
	AvgThree(p0[0], p1[0], p2[0]), 
	AvgThree(p0[1], p1[1], p2[1]), 
	AvgThree(p0[2], p1[2], p2[2])];
function CenterOfGravity4(p0, p1, p2, p3) = [
	AvgFour(p0[0], p1[0], p2[0], p3[0]), 
	AvgFour(p0[1], p1[1], p2[1], p3[1]), 
	AvgFour(p0[2], p1[2], p2[2], p3[2])];
function CenterOfGravity5(p0, p1, p2, p3, p4) = [
	AvgFive(p0[0], p1[0], p2[0], p3[0], p4[0]), 
	AvgFive(p0[1], p1[1], p2[1], p3[1], p4[1]), 
	AvgFive(p0[2], p1[2], p2[2], p3[2], p4[2])];
function CenterOfGravity6(p0, p1, p2, p3, p4, p5) = [
	AvgSix(p0[0], p1[0], p2[0], p3[0], p4[0], p5[0]), 
	AvgSix(p0[1], p1[1], p2[1], p3[1], p4[1], p5[0]), 
	AvgSix(p0[2], p1[2], p2[2], p3[2], p4[2], p5[0])];

// FROM HERE THE ACTUAL RENDERING

module vertex_edge_holder(angle)
{
	difference() {
		// compensate for the previous rotation
		translate([0, -radius*cos(angle)-thickness*(sin(angle)+0.5), radius*sin(angle)+0*thickness*cos(angle)])
		// rotate the edges
		rotate ([angle,0,0])
		// make the cylinder ellpitical to compensate for wall thickness
		scale([1,(radius*cos(angle)+thickness)/(radius + thickness),1])
		// work with double length elements, will be truncated
		translate([0,0,-1*length]){
			difference() {
				union(){
					cylinder(h = 2*length, r = radius + thickness);
					translate([-0.5*sqrt(2)*(radius+thickness),0,0])
						cube([sqrt(2)*(radius+thickness),2*length,2*length]);
				}
				translate([(angle<45)?-0.5:-0.5*radius, -2*length-radius, length])
					cube([(angle<45)?1:radius,2*length,2*length]);
			}
		}

		// remove all excess connector material
		translate([-2.5*length,m,-2.5*length])
			cube(5*length);
	}
}

module vertex_edge(angle)
{
	translate([0, -radius*cos(angle)-thickness*(sin(angle)+0.5), radius*sin(angle)+0*thickness*cos(angle)])
		rotate ([angle,0,0])
			cylinder(5*length, radius, radius);
}

module vertex(params)
{
	normal = params[0];
	origin = params[1];
	endpoints = params[2];

	// construct new coordinate system based on supplied normal or the origin location
	zdir = VMAG(normal) > 0 ? VNORM(normal) : VNORM(VINV(origin));
	ydir = -VNORM(VCROSS(zdir, VSUB(endpoints[0],origin)));
	xdir = -VNORM(VCROSS(zdir, ydir));

//	// uncomment for an example of the rotation
//	// rotation to put zdir on z axis
//	zrotate = [(zdir[2]==0 && zdir[1]==0) ? 0 : atan2(zdir[1],zdir[2]), acos(zdir[0])-90, 0];
//	rotate(zrotate)
//	{
//		cyl([0,0,0],xdir,40,0.5);
//		cyl([0,0,0],ydir,40,0.5);
//		cyl([0,0,0],zdir,40,0.5);
//	}

	//dimensions of the connector are based upon the first edge
	angle = VANG(zdir,VSUB(endpoints[0],origin));
	height = cos(angle)*(length + 0*thickness) + 2 * radius * sin(angle);

	//adjust angles for easy printing
	mirror((angle>45)?[0,0,1]:[0,0,0])
	translate((angle>45)?[0,0,-height]:[0,0,0])

	//create the vertex
	intersection()
	{
		difference()
		{
			union(){
				for (endpoint = endpoints)
				{
					rotate([0,0,VSANG(xdir,VSUB(endpoint,origin),zdir)+90])
						vertex_edge_holder(VANG(zdir,VSUB(endpoint,origin)));
				}
				if (VMAG(normal) == 0)
				{
					cylinder(5*length,radius+thickness,radius+thickness,true);
				}
			}
			for (endpoint = endpoints)
			{
				rotate([0,0,VSANG(xdir,VSUB(endpoint,origin),zdir)+90])
					vertex_edge(VANG(zdir,VSUB(endpoint,origin)));
			}
			if (VMAG(normal) == 0)
			{
				cylinder(5*length,radius,radius,true);
			}
		}
		//remove excess material
		cylinder(height, 5*length, 5*length);	
	}
}



20110722_nudo_ng_star_v1_detail_preview_medium.jpg 20110727_tetraocta_grid_01_preview_medium.jpg 20110727_tetraocta_grid_02_preview_medium.jpg 20110727_tetraocta_grid_03_preview_medium.jpg
Tetra-octahedral bars & nodes grid structure

cutaway_hexagon_8_preview_medium.jpg DSCF2995_preview_medium.jpg
Cutaway, Hollow Elements

DSCF2995_preview_medium.jpg
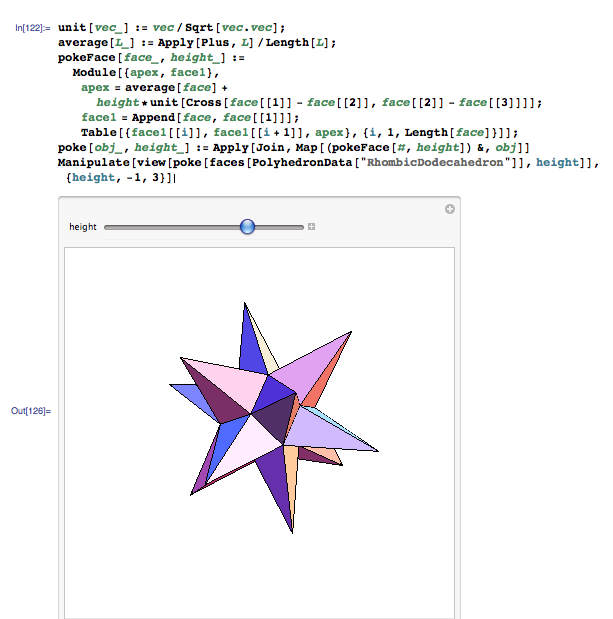
Polyhedron Facets

DSCF2648_preview_medium.jpg
Snap-together polyhedron verticies

DSC03073_preview_medium.jpg DSC03074_preview_medium.jpg
Face-centered Cubic Voroni Tetrahedron

DSC_0095_preview_medium.jpg
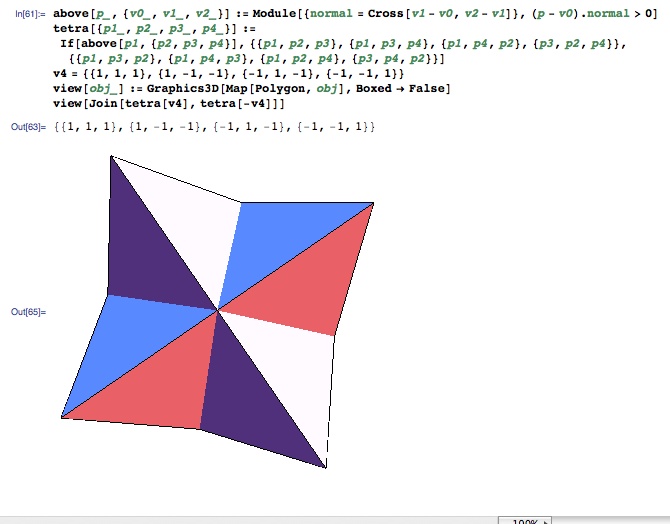
Stellated octahedron