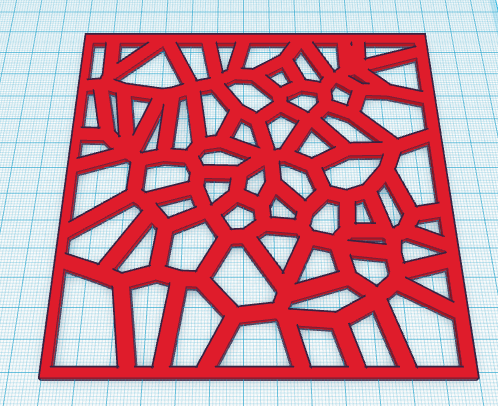
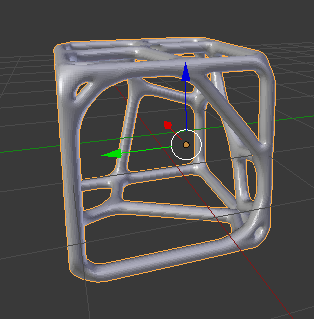
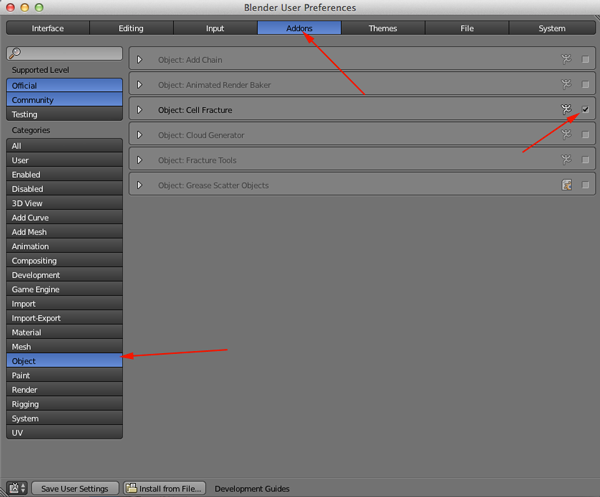
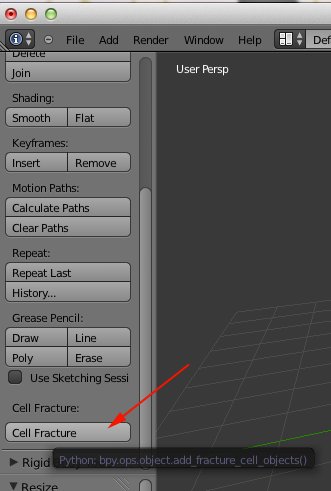
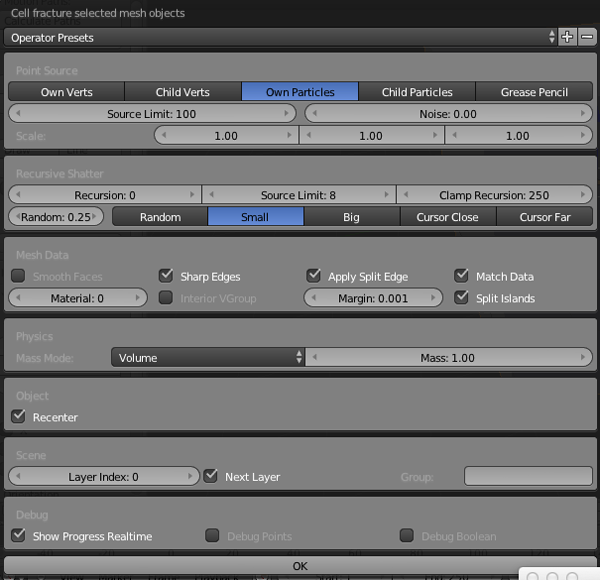
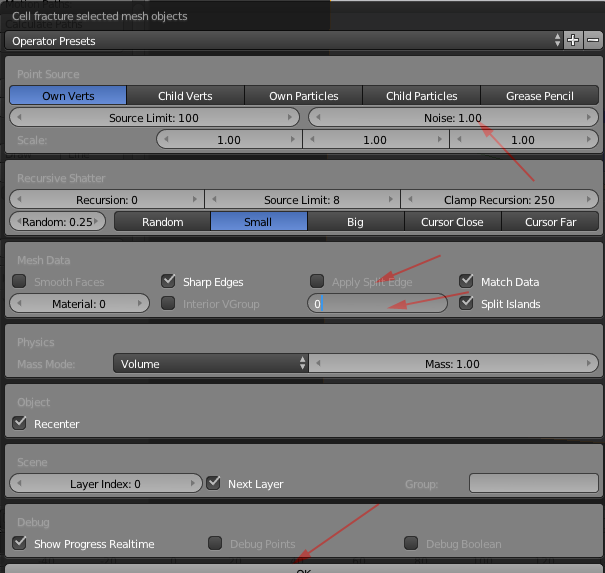
Voronoi Diagrams
Grades 8-12-
 Art
Art  Math
Math
Introduction
 Image from project2gether.com |
 Image from thingfuture.com |

Image from 3dsoup.com |
 © 3Dizingof.com Image from Adafruit |

Image from ink361.com |
A Dirichlet tessellation, or Voronoi diagram, is a partitioning of a plane containing a set of points into convex polygons such thatThe individual cells resulting from this process are known as Dirichlet regions, Thiessen polytopes, or Voronoi polygons.
- each polygon contains exactly one generating point
- every point in a given polygon is closer to its generating point than to any other
Voronoi diagrams were considered as early as 1644 by René Descartes and were used in 1850 by Lejeune Dirichlet in the investigation of positive quadratic forms. They were also studied by Georgy Voronoi in 1907. Voronoi diagrams find widespread applications in areas such as computer graphics, epidemiology, geophysics, and meteorology. A particularly notable use of Voronoi diagrams is the analysis of the 1854 Cholera epidemic in London, in which physician John Snow determined a strong correlation between death rates and proximity to the infected Broad Street water pump.
Voronoi Diagrams from the Wolfram Demonstrations Project by Ed Pegg Jr
The Facilities Location Problem from the Wolfram Demonstrations Project by Tim Neuman
Voronoi diagrams have a wide range of uses from calculating the area per tree in the forest, to determining the source of Cholera. In general these diagrams are useful for finding "who is closest to whom." Voronoi diagrams are used:
- Path planning in the presence of obstacles
- Model and analyze plant competition
- Analyzing patterns of urban settlements
- Geometric modeling
- Closest pairs algorithms
- Nearest-neighbor queries
Say you have a map of your city, and on it you have located a set of points representing every fast food restaurant. Creating a Voronoi diagram from these points would enable you (on your walk through the city) to know which restaurant you're closest to at any given time. Of course, an application that simple could be solved more efficiently via other methods, but let's raise the stakes a bit. What if you want to know the percentage of your walk that will be closest to one particular McDonalds. Suddenly, without a Voronoi diagram, this is tricky. With a Voronoi diagram, however, it's a simple matter of intersecting the line that represents your walk with the cell that surrounds that particular restaurant.
Voronoi diagrams can also be used to make maps, not just analyze them. Say you have a set of points that represent air quality sample locations. To quickly generalize the sample points into a local map… bam! Voronoi diagram!
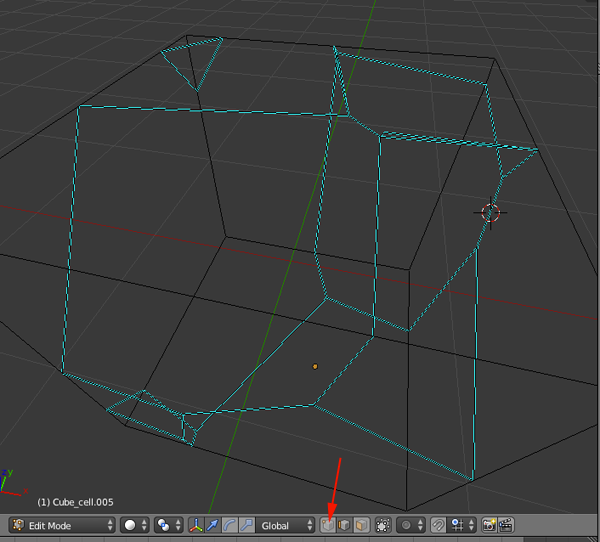
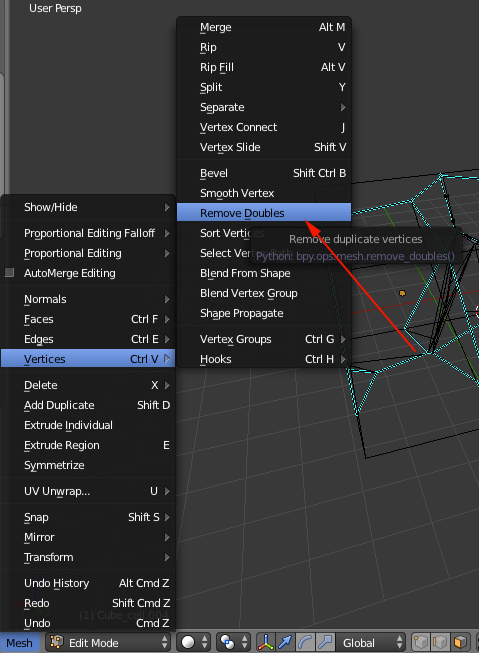
How to Draw A Voronoi Cell
First way: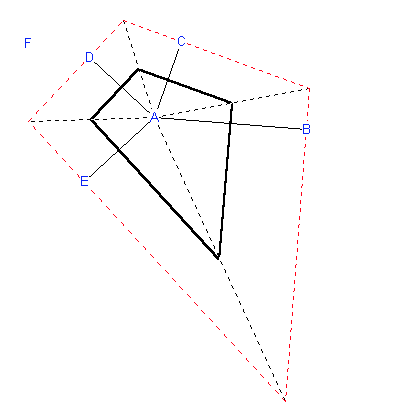
Image frommathforum.org
Start with a figure of six points ABCDE (F comes later). To construct the Voronoi cell of A draw the perpendicular bisectors of segments AB, AC, AD, and AE. These perpendicular bisectors enclose a polygon around point A. In the figure above this polygon is the bold black quadrilateral. Only the sides of this polygon form the cell around A. The rest can be removed (as is done in the figure).
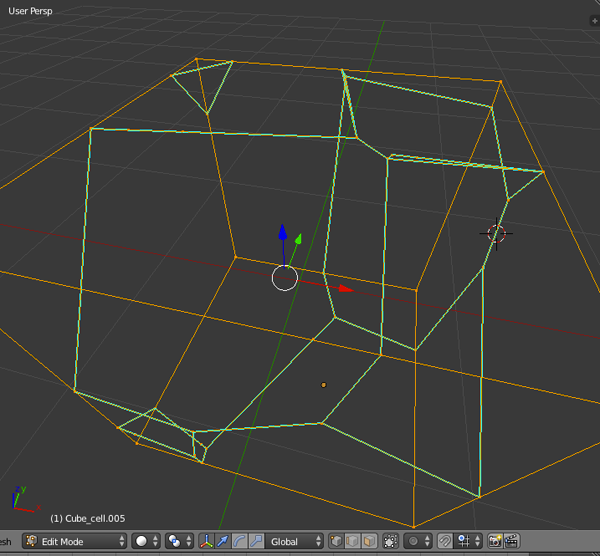
from Second way:
- Input Sites.
- Connect Nearest Neighbors (shortest line wins).
- Find Center Points.
- Draw Perpendicular Bisectors.
- Trace Cells.

Images from sevensixfive
Use different colors for the input sites, the Delauney lines, and the bisectors.
- The input points, step one, are called sites, labeled here A, B, C, etc.
- Connect the sites to all of their nearest neighbors without making a line that crosses another. This is known technically as the Delauney Triangulation.
- Find and mark the centerpoint of every line on the Delauney graph.
- Draw the perpendicular bisector for each Delauney line. This is where careful accuracy, in finding the centerpoints, and in drawing a tight 90 degree angle, pays off. If everything has been done correctly, there will always be three lines converging at a point, unless the input sites are on a perfectly regular rectangular grid.
- Retrace the outline of each Voronoi cell from the perpendicular bisectors. There will be one cell for every site, and at the end, each cell is just the set of all surface area points that are closer to its site than any of the other sites, as illustrated in the last panel: A' -> A, B' -> B, etc.
Lesson Purpose
- To explore voronoi cells.
- To create art with math.
Materials
- 3D printer
- Access to the internet.
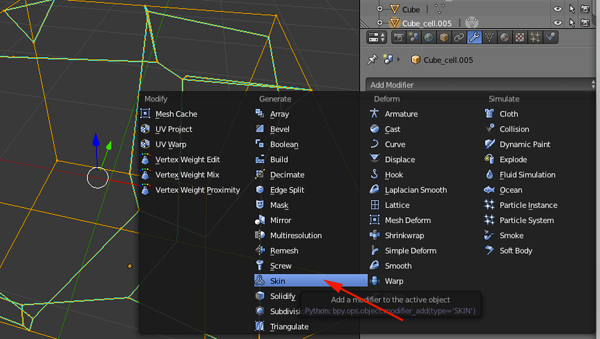
- Applications: MeshLab, Blender, TinkerCad
Resources
- Wolfram MathWorld
- Wolfram Demonstration Project
- Voronoi Diagrams: Applications from Archaology to Zoology
- zheng3's Meshlab tutorial
- sevensixfiveLHow to: Draw the Voronoi Diagram
- codeproject: Create a Voronoi Diagram
- Mesh—A Processing Library
- Don Havey's Voronoi Diagram tutorial
- Voronoi Encapsulation, Walk Through (How to) using Blender & 3D Printing the result Gareth Chiprobot
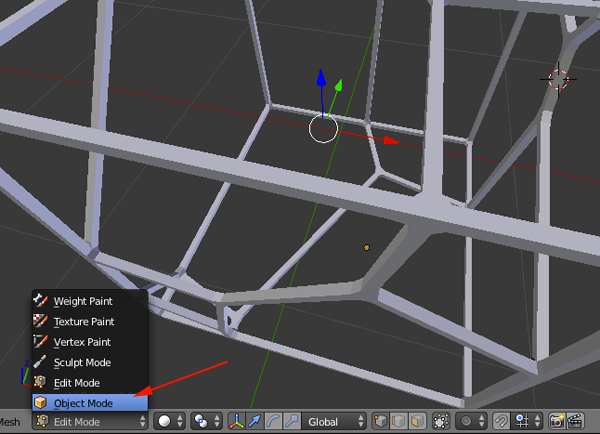
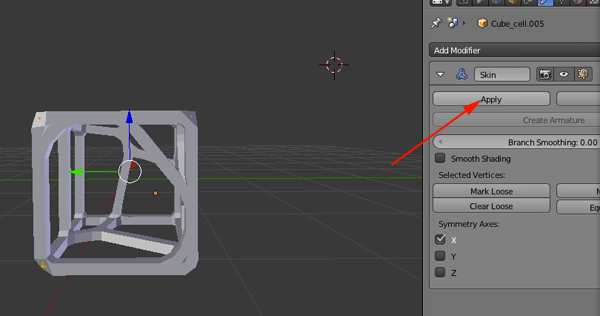
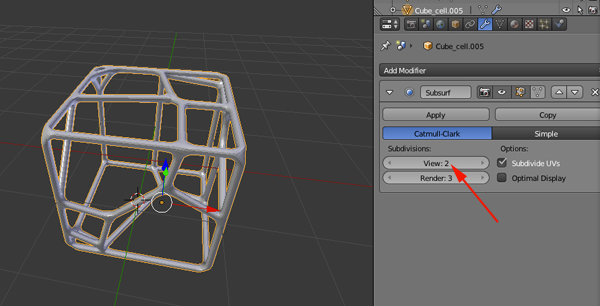
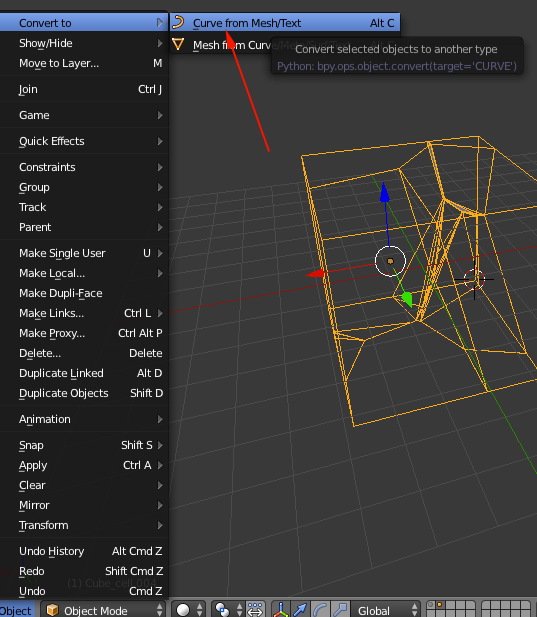
Procedure

- Open MeshLab
- Import or add a new form:Filters>Create New Mesh Layer>some_form
- Turn on flat lines
- Enable Layers. This will bring up the Layers sidebar.
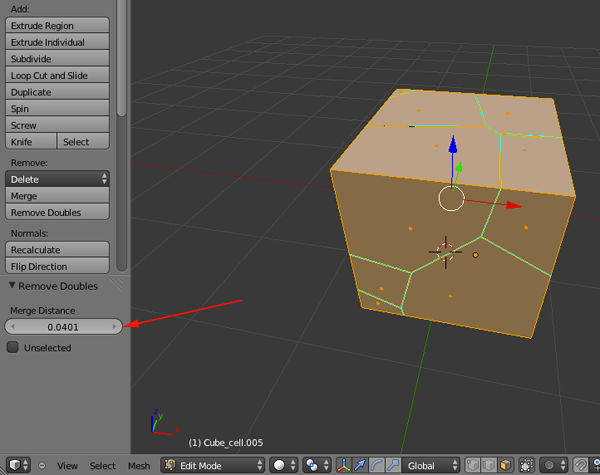
- You want around 300k faces so select Filter>Remeshing>Subdivision surfaces:Loop or midpoint.
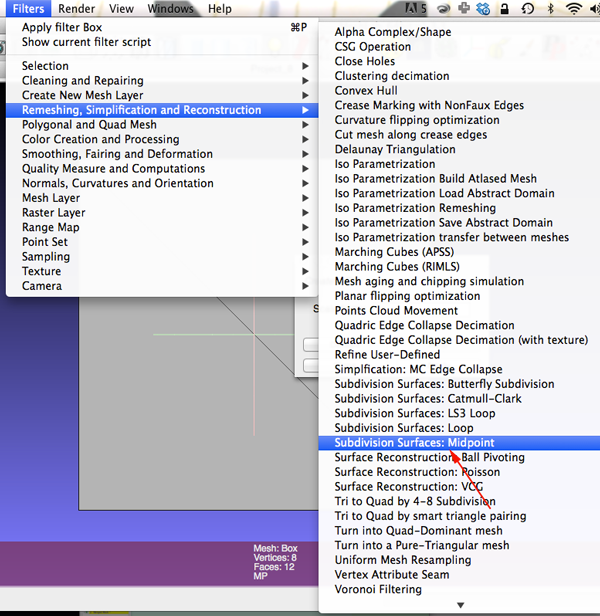
- Change the perc field to .5
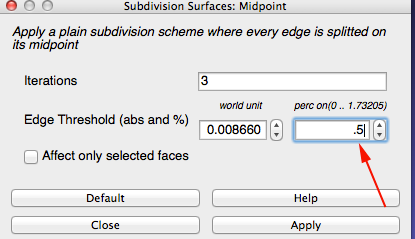
- Keep clicking on Apply until you get close to 300k faces
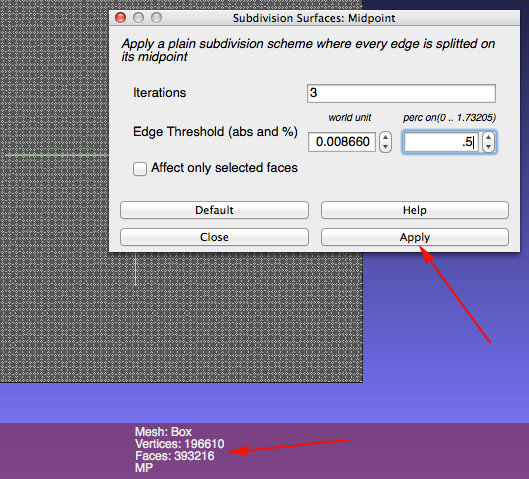
- Select Filter>Sampling>Poisson Disk Sampling
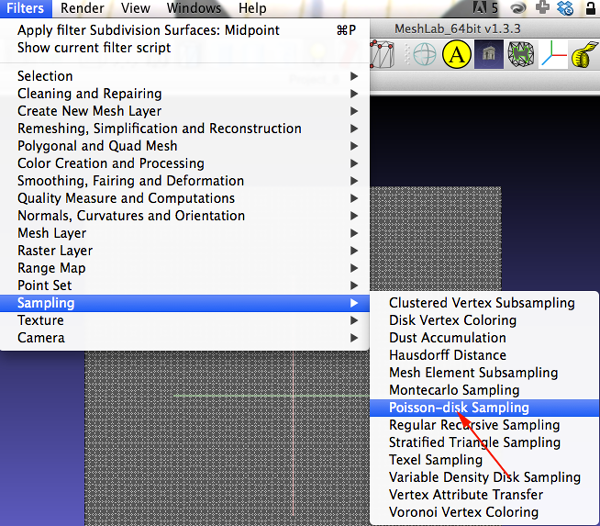
- In the dialog box enter 35
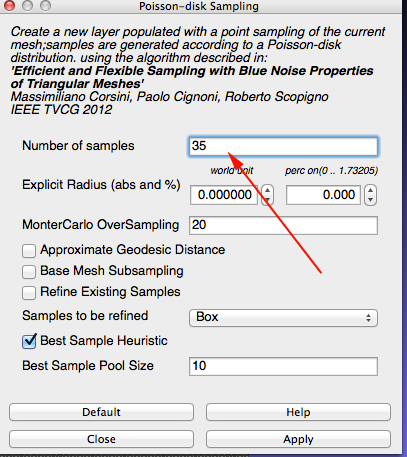
You are looking for about 50 points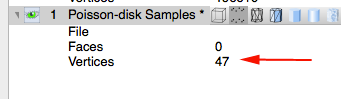
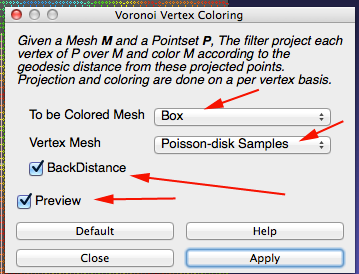
The points represent your sites - Select Filter>Sampling>Voronoi Vertex Coloring
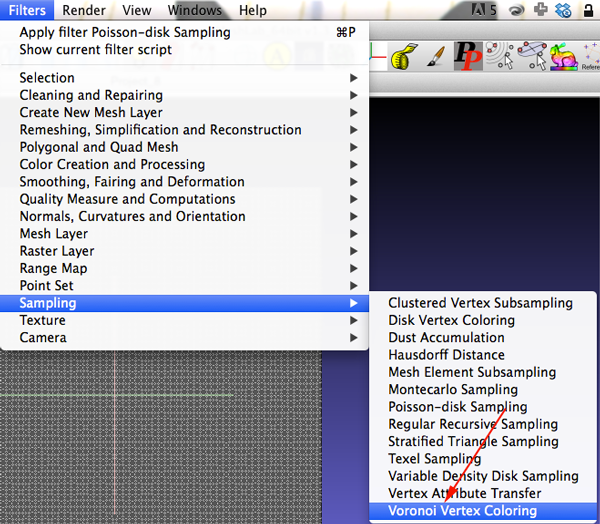
- Make sure your dialog box is set up similar to the one below:
- CTRL+click on the top layer and select Flatten Visible Layers
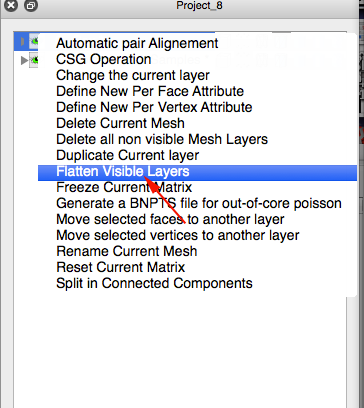
- Apply flatten
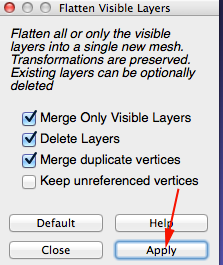
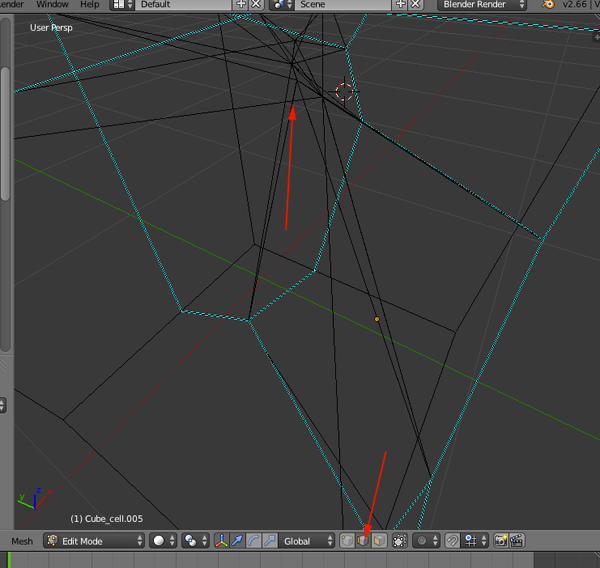
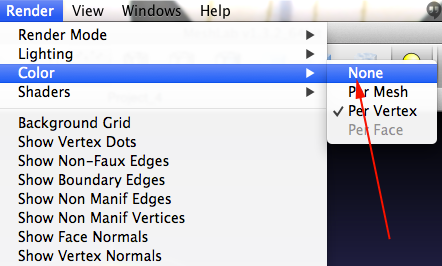
- Remove the interior faces. First click on
Render>Color>None
- Select Filters>Selection>Select Faces by Vertex Quality
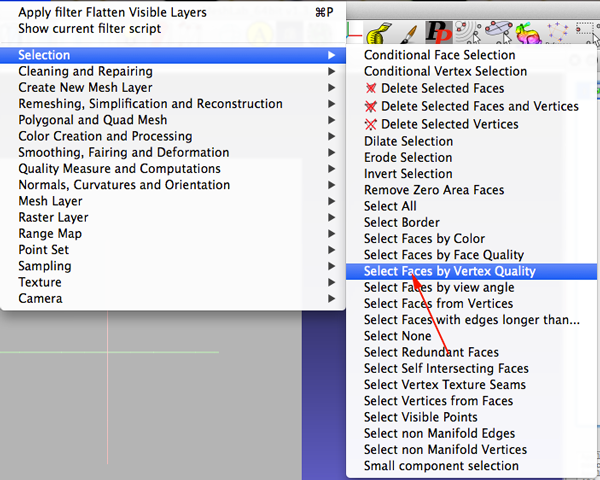
- Check the Preview checkbox and adjust the sliders
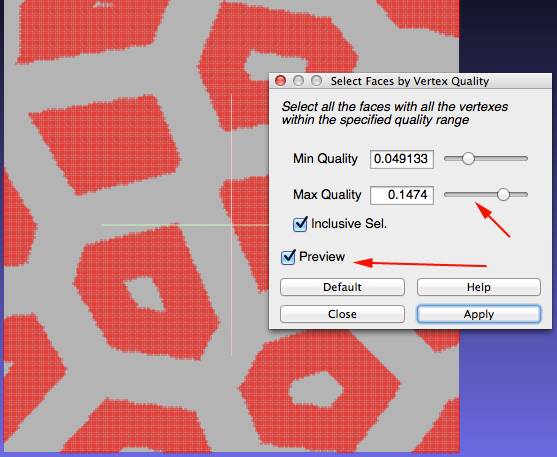
- Keep adjusting until the selection looks the way you want it to. Click apply and then close the selection window.
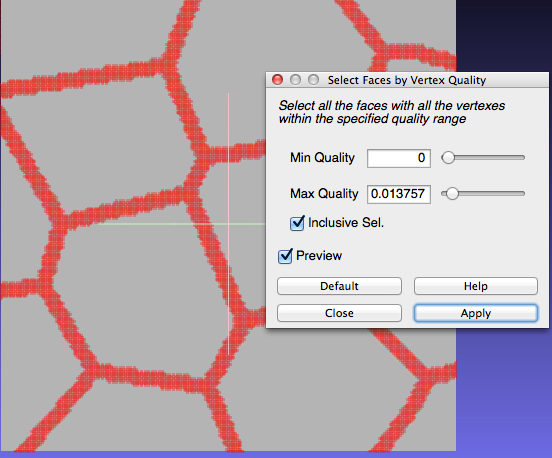
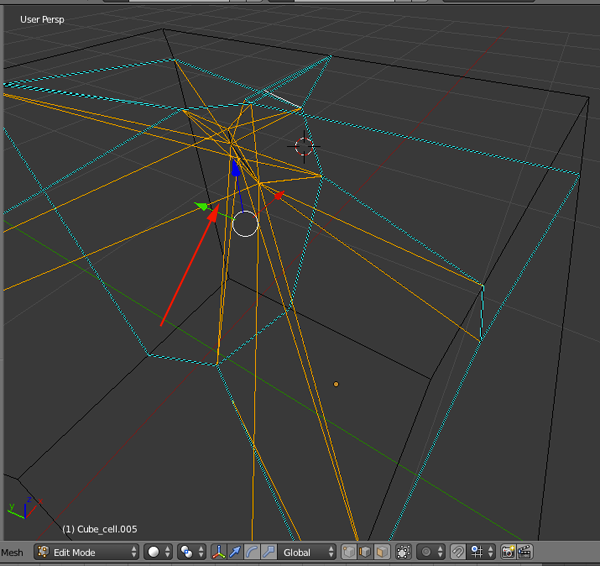
- Select Filter>Selection>Invert Selection
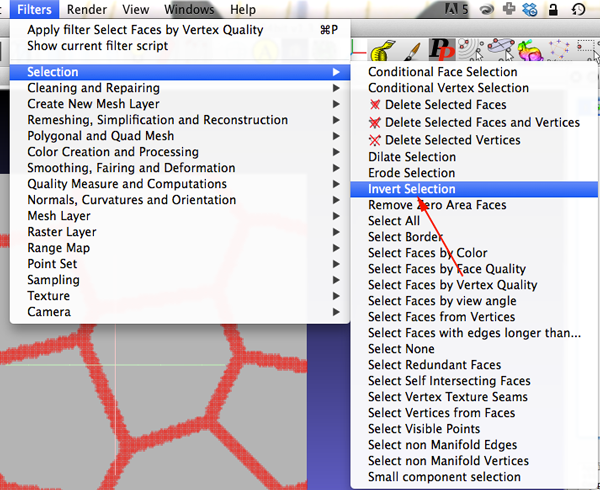
- Apply the Inversion
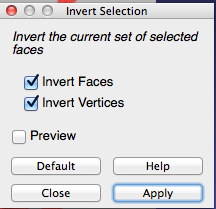
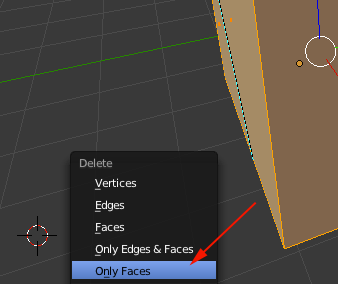
- Click the Delete Faces button.
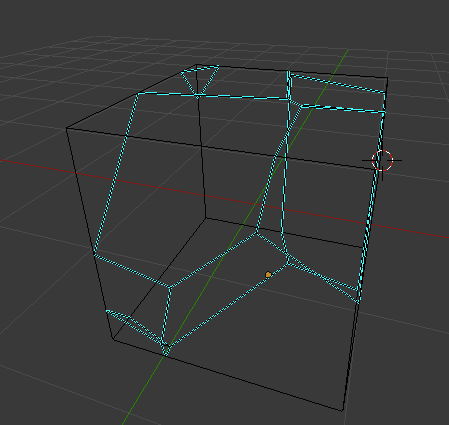
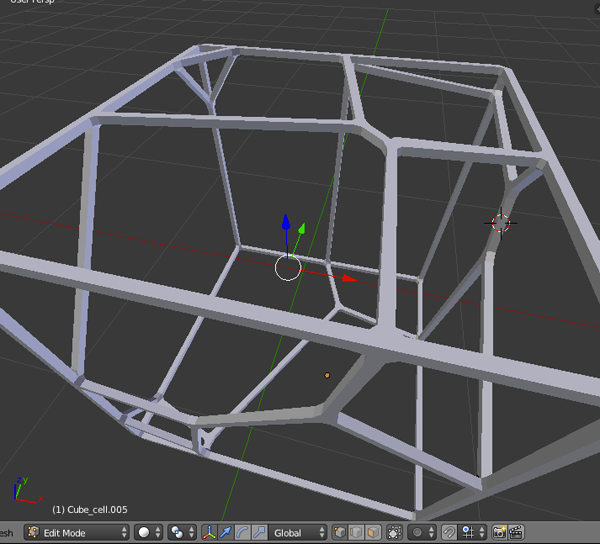
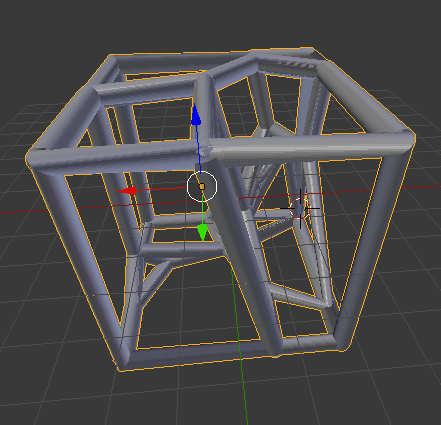
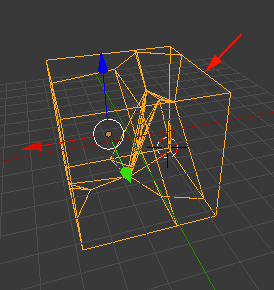
- You should have a single-sided Voronoi mesh.

- Time to refine the mesh. Select Filters>Smoothing, Fairing, and Deformation>Laplacian Smooth.
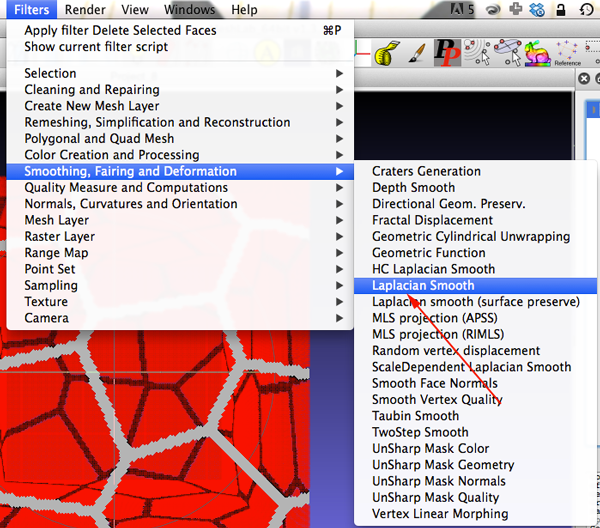
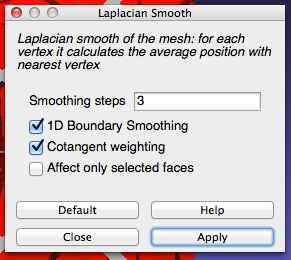
- Apply the filter
- You still have just a 2D mesh. You need to extrude the mesh. Select Filters>Remeshing, Simplification, and Reconstruction>Uniform Surface Resampling
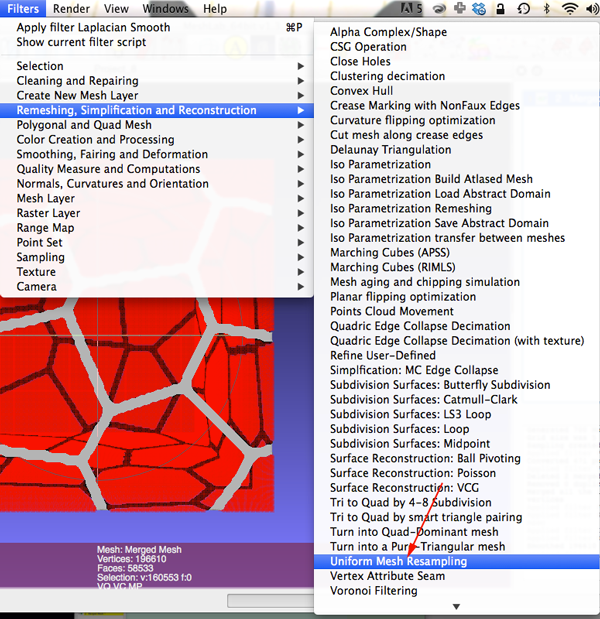
- Make sure your dialog box looks similar
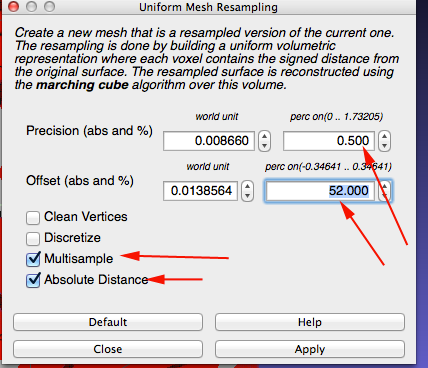
- Click Apply. This will take some time to process. Be patient.
- Turn off the layer that is not the offset layer./li>
- Select the Offset layer. One last smothing algorithm: select Filters>Smoothing, Fairing, and Deformation>Taubin Smooth.
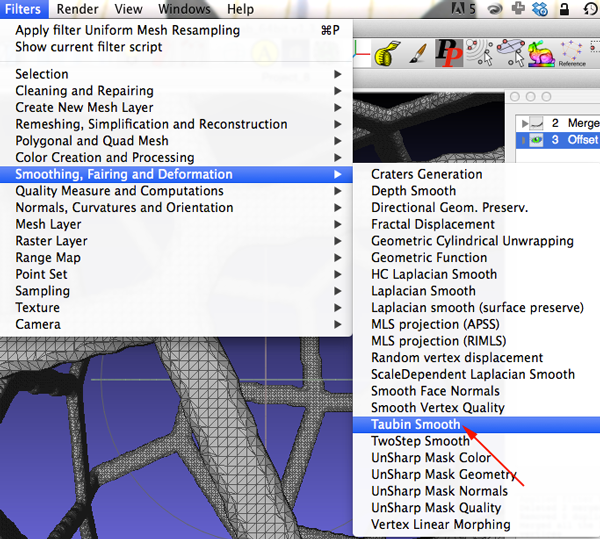
- Keep the defaults and apply Taubin filter
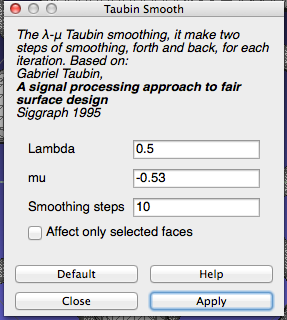
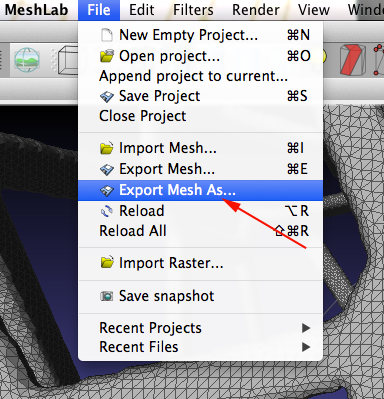
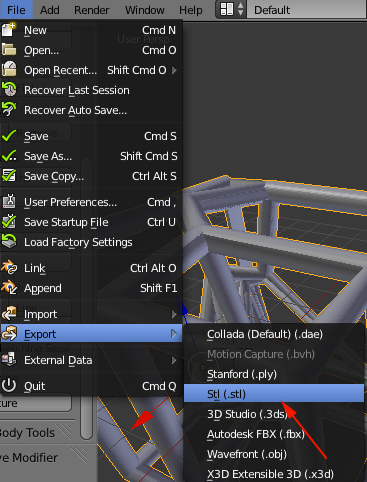
- Export As and save as an STL