Setting Hamlet
Lesson by:Dara Ross
The Brooklyn International High School
9th and 10th Grade Humanities
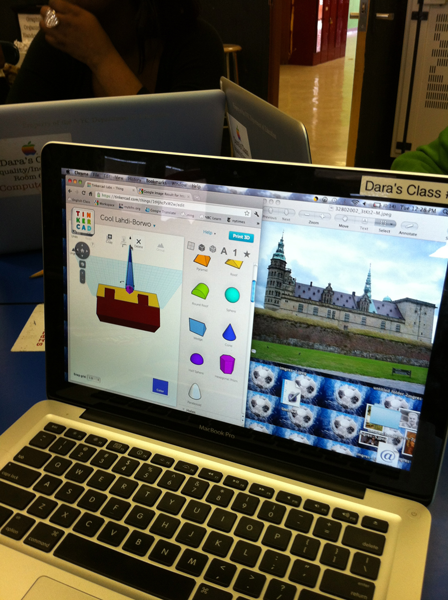

 Thingiverse:thing:17533
Thingiverse:thing:17533
Aim
How can we understand setting?
Objective
Students will use tinkercad.com and to research and analyze Elsinore Castle in Denmark, the setting of the play
Hamlet by William Shakespeare.
Materials Needed
-
- Computers with internet access
- Tinkercad.com (free)
- Google Earth
- Google Maps
- Makerbot
Description
While or after reading the play tell students that even though the story of Hamlet is fictional, the setting of Hamlet is real. Have students research the setting of Hamlet, Elsinore castle. The students can use the “Setting Hamlet” graphic organizer to help guide their research. Students can then draw and recreate the castle using Tinkercad.
Assessment
-
Rubric
New York State Learning Standards
Common Core Standards
-
Reading
| 10.2: Literature Key Ideas and Details
| Determine a theme or central idea of a text and analyze in detail its development over the course of the text, including how it emerges and is shaped and refined by specific details; provide an objective summary of the text.
| √ |
| 10.8: Reading: Informational Text
| Delineate and evaluate the argument and specific claims in a text, assessing whether the reasoning is valid and the evidence is relevant and sufficient; identify false statements and fallacious reasoning.
| √ |
Math Common Core Standards
-
Congruence
| G.CO.12 | Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). | √ |
-
Modeling with Geometry
| G.MG.1 | Apply geometric concepts in modeling situations
1. Use geometric shapes, their measures, and their properties to describe objects
| √ |
-
Geometric Measurement & Dimension
| G.GMD.4 | Visualize relationships between two-dimensional and three-dimensional objects
Identify the shapes of two-dimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects.
| √ |



