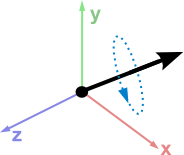
The quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. A feature of quaternions is that the product of two quaternions is noncommutative. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space or equivalently as the quotient of two vectors. Quaternions can also be represented as the sum of a scalar and a vector (wikipedia).
Any rotation in three dimensions can be represented as a combination of an axis vector and an angle of rotation. Quaternions give a simple way to encode this axis-angle representation in four numbers and apply the corresponding rotation to a position vector representing a point relative to the origin in R3(wikipedia).
A quaternion represents two things with four numbers:
The magnitude is one for the unit quaternion. If you have to normalize a quaternion:
Performing the above operations ensures that the quaternion is a unit quaternion. There are many different possible unit quaternions - they actually describe a hyper-sphere, or a four dimensional sphere. But because the end points for unit quaternions all lay on a hyper-sphere, multiplying one unit quaternion by another unit quaternion will result in a third unit quaternion.
Here is how the multiplication itself is performed:
Let Q1 and Q2 be two quaternions, which are defined, respectively, as (w1, x1, y1, z1) and (w2, x2, y2, z2).
Quaternion multiplication is not commutative.
What does the quaternion multiplication mean? A quaternion stores an axis and the amount of rotation about that axis. To change the rotation represented by a quaternion, a few steps are necessary. First, you must generate a temporary quaternion, which will simply represent how you're changing the rotation. If you're changing the current rotation by rotating backwards over the X-axis a little bit, this temporary quaternion will represent that. By multiplying the two quaternions (the temporary and permanent quaternions) together, you will get a new permanent quaternion, which has been changed by the rotation described in the temporary quaternion.
To generate the temp_rotation, you'll need to have the axis and angle prepared, and this will convert them to a quaternion. Here's the formula for generating the temp_rotation quaternion.
Then, multiply temp_rotation by total. Since you'll be multiplying two unit quaternions together, the result will be a unit quaternion. You won't need to normalize it.
Generate the matrix from the quaternion to rotate your points.
And, since we're only dealing with unit quaternions, that matrix can be optimized a bit down to this:
For more information about quaternions:
member WilliamAAdams created code to add quaternions to OpenSCAD. Using Adams's code will allow you to do the following:
To do a 30 degree rotation around the z-axis for example:
You need to turn it into a matrix that OpenSCAD can easily use and apply as a transform:
Once you have this, you can use it with multmatrix()
Combinations can be done like this:
This combines the 30 degree rotation around the z-axis, followed by the 15 degree rotation about the y-axis, or visa versa.
Any rotation in three dimensions can be represented as a combination of an axis vector and an angle of rotation. Quaternions give a simple way to encode this axis-angle representation in four numbers and apply the corresponding rotation to a position vector representing a point relative to the origin in R3(wikipedia).
A quaternion represents two things with four numbers:
- an axis of rotation
- an amount of rotation about the axis
magnitude = sqrt(w2 + x2 + y2 + z2)
magnitude = sqrt(w2 + x2 + y2 + z2) w = w / magnitude x = x / magnitude y = y / magnitude z = z / magnitude
Quaternion Multiplication
One of the most important operations with a quaternion is multiplication. When you have two quaternions, and you multiply them with each other, the rotations are merged into a single rotation. If you want to apply successive rotations to a model, you multiply all the respective quaternions representing these rotations with each other, and end up with a single quaternion.
Here is how the multiplication itself is performed:
Let Q1 and Q2 be two quaternions, which are defined, respectively, as (w1, x1, y1, z1) and (w2, x2, y2, z2).
(Q1 * Q2).w = (w1w2 - x1x2 - y1y2 - z1z2) (Q1 * Q2).x = (w1x2 + x1w2 + y1z2 - z1y2) (Q1 * Q2).y = (w1y2 - x1z2 + y1w2 + z1x2) (Q1 * Q2).z = (w1z2 + x1y - y1x2 + z1w2
What does the quaternion multiplication mean? A quaternion stores an axis and the amount of rotation about that axis. To change the rotation represented by a quaternion, a few steps are necessary. First, you must generate a temporary quaternion, which will simply represent how you're changing the rotation. If you're changing the current rotation by rotating backwards over the X-axis a little bit, this temporary quaternion will represent that. By multiplying the two quaternions (the temporary and permanent quaternions) together, you will get a new permanent quaternion, which has been changed by the rotation described in the temporary quaternion.
// generate a temp_rotation total = temp_rotation * total //multiplication order matters on this line
//axis is a unit vector temp_rotation.w = cosf( fAngle/2) temp_rotation.x = axis.x * sinf( fAngle/2 ) temp_rotation.y = axis.y * sinf( fAngle/2 ) temp_rotation.z = axis.z * sinf( fAngle/2 )
Generate the matrix from the quaternion to rotate your points.
| w2+x2-y2-z2 | 2xy-2wz | 2xz+2wy | 0 |
| 2xy+2wz | w2-x2+y2-z2 | 2yz+2wx | 0 |
| 2xz-2wy | 2yz-2wx | w2-x2-y2+z2 | 0 |
| 0 | 0 | 0 | 1 |
And, since we're only dealing with unit quaternions, that matrix can be optimized a bit down to this:
| 1-2y2-2z2 | 2xy-2wz | 2xz+2wy | 0 |
| 2xy+2wz | 1-2x2-2z2 | 2yz+2wx | 0 |
| 2xz-2wy | 2yz-2wx | 1-2x2-2y2 | 0 |
| 0 | 0 | 0 | 1 |
For more information about quaternions:
member WilliamAAdams created code to add quaternions to OpenSCAD. Using Adams's code will allow you to do the following:
myquat = quat(axis, angle);
rotz = quat([0,0,1], 30);
rotzmatrix = quat_to_mat4(rotz);
multmatrix(rotzmatrix);
multmatrix(quat_to_mat4(quat([0,0,1],30)));
q1 = quat([0,0,1],30); q2 = quat([0,1,0], 15); combo = quat_mult(q1, q2); multmatrix(quat_to_mat4(combo));
Instructions
- Download maths.scad and test_maths.scad
- Play around with the test_maths.scad file to see how to use it
